图像处理
图像处理基础 Image process basics
图片的频率
该部分内容参考自 VCB-Studio 公开教程
可参考这一部分内容来简要了解老师在课程中提到的高频信息、低频信息
图片中像素变化较快,变动幅度大的区域,高频分量占据主导地位。像素变化缓慢,变化幅度小的区域,低频分量占据主导地位。

平面:
平面 (flat areas) 是包含大量低频分量的区域,其特点是像素变化非常小。如上图左侧黄框区域。
线条:
线条 (lines) 是包含极端高频分量的区域,其像素有跳跃式的急剧变化。如上图中间红框区域。
纹理:
纹理 (texture) 区域较为复杂,其像素在小范围内频繁变化,高低起伏不断。纹理变化剧烈的,称之为强纹理,中高频成分占据主导,其性质接近于线条。如上图左侧蓝框区域。纹理变化平缓的,称之为弱纹理,中低频率成分占据主导,其性质接近于平面。如上图右侧绿框区域。
噪点:
噪点 (noise) 是一类特殊的画面要素,表现为随机的像素涨落,它可以叠加到以上任意要素中。噪点的频率构成取决于其种类,白噪声在各个频率的强度完全一致,而一般动画原盘所带的噪点则涵盖低频到中高频,随频率增高而略有下降,最高频部分则基本被砍掉。
调整图像对比度
提高对比度就是让图片亮的地方更亮,暗的地方更暗

通过 S 曲线实现亮度的重新映射
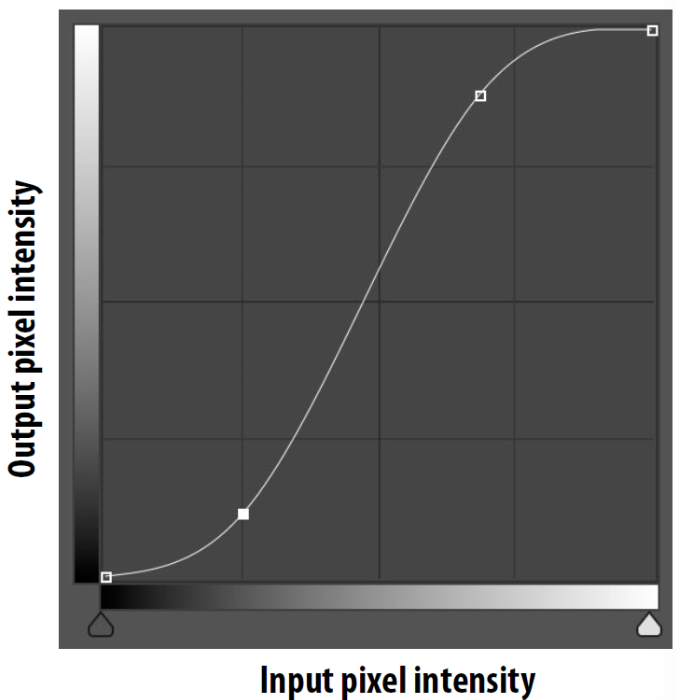
图像颜色反转 invert

图像模糊 blur
去除图像中的高频部分

也可以不对边缘进行模糊以实现更“智能”的模糊效果
图像锐化 sharpen
增强图像中的高频部分

图像边缘检测 edge detection
提取图像中的高频部分

卷积 convolution
无需记忆公式,只需要知道卷积核在被卷积的张量上以步长的长度移动即可
在不进行 padding 的情况下,卷积后输出的尺寸为:
其中 W 表示输入尺寸 (如:长度、宽度),F 表示卷积核大小,S 表示步长
填充 padding
Zero values 填充 0
Edge values 填充边界值
Symmetric 以与边界的对称方式填充
模糊 blur
Box Blur
使用卷积完成每个像素与周围像素的均值操作均值操作

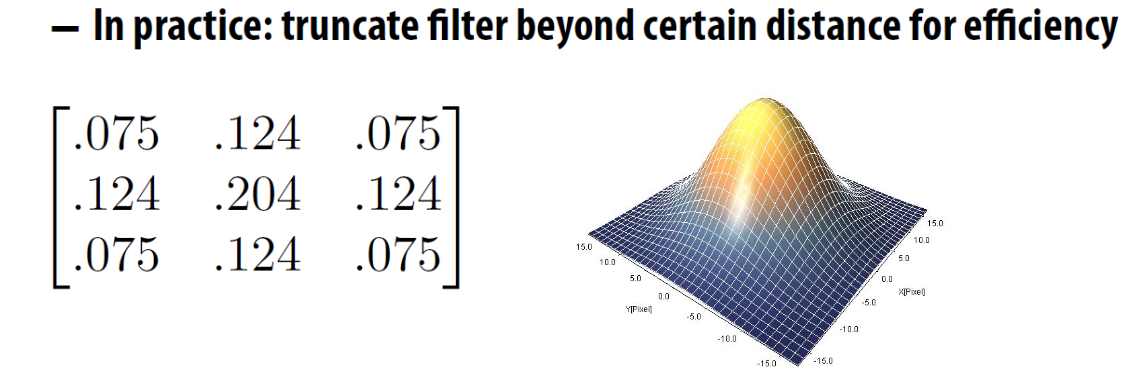
高斯模糊 Gaussian blur
二维高斯公式:
卷积核由高斯公式计算得到,其中,使用的高斯公式越平缓 (尖峰部分越矮),模糊效果越明显

锐化 sharpen
I 表示原始图像的信息
图像中的高频信息:
锐化后的图像信息:
可行的卷积核:
边缘检测
梯度检测滤波器
垂直边缘检测:
实际的卷积核形状也更像垂直边缘 (左黑右白)
水平边缘检测:
实际的卷积核形状更像水平边缘 (上黑下白)
由此可以看出,使用卷积核对图像进行卷积操作时,与卷积核形状更相似的部分会产生更大的相应

双边滤波器 Bilateral filter
了解即可
在保留边缘的情况下,对图像的其他部分进行高斯模糊以实现去噪


图像采样 Image sampling
图像分辨率
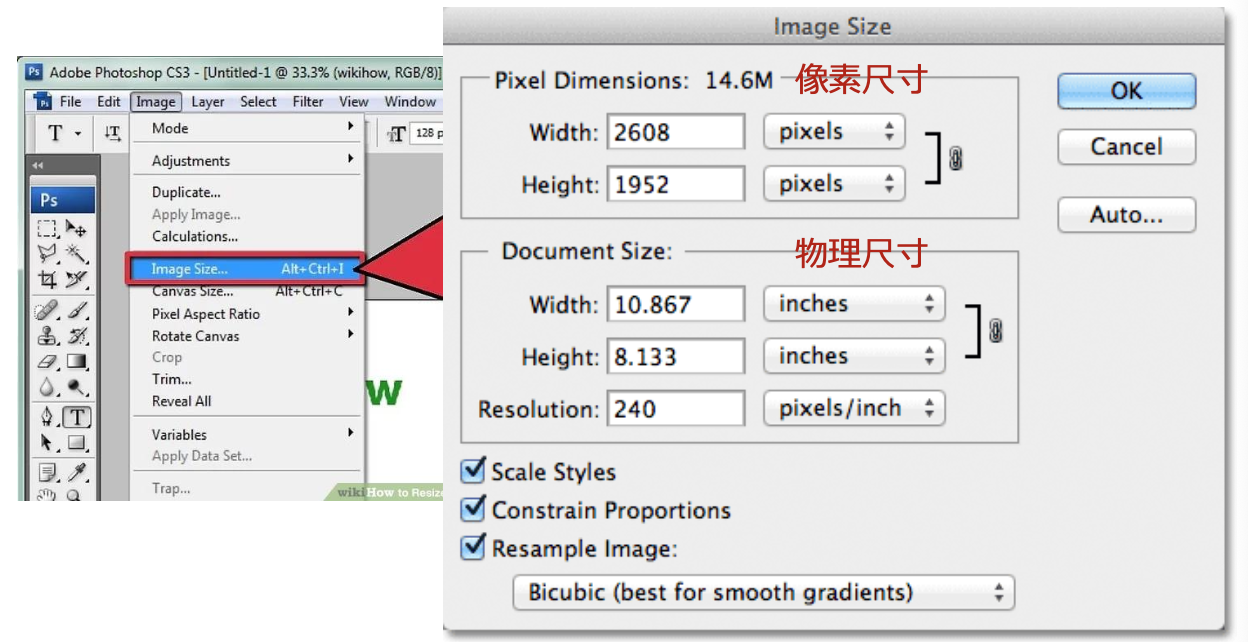
图像包含像素尺寸和物理尺寸
像素尺寸顾名思义,单位为像素,不具有物理意义上的大小含义
物理尺寸,表示图像的物理大小,单位可为英寸 (inch)
这二者之间的联系即为分辨率 (resolution),单位为像素每英寸 (pixels/inch, PPI)
降采样 Down sampling
能减小图片的大小
每隔一点采样一次,可以实现将图像的大小缩小为原来的一半
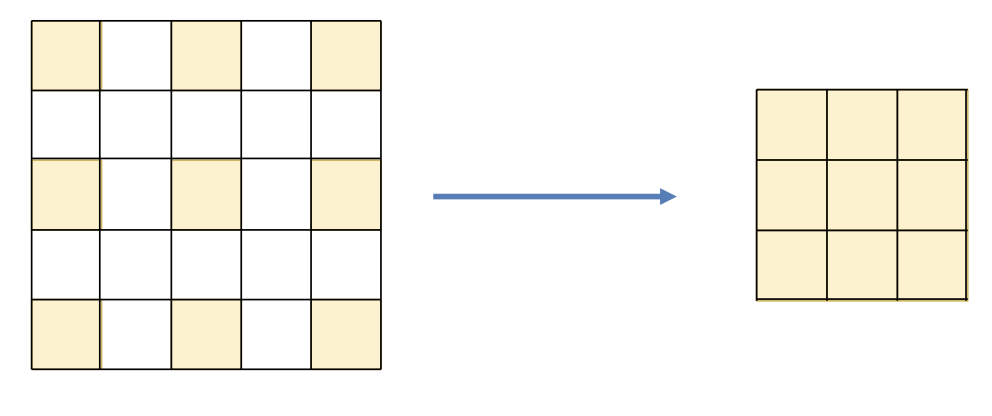
同时也会造成一些信息的丢失,出现混叠现象
混叠 Aliasing
由于信号变化的频率过快或采样的频率过低导致
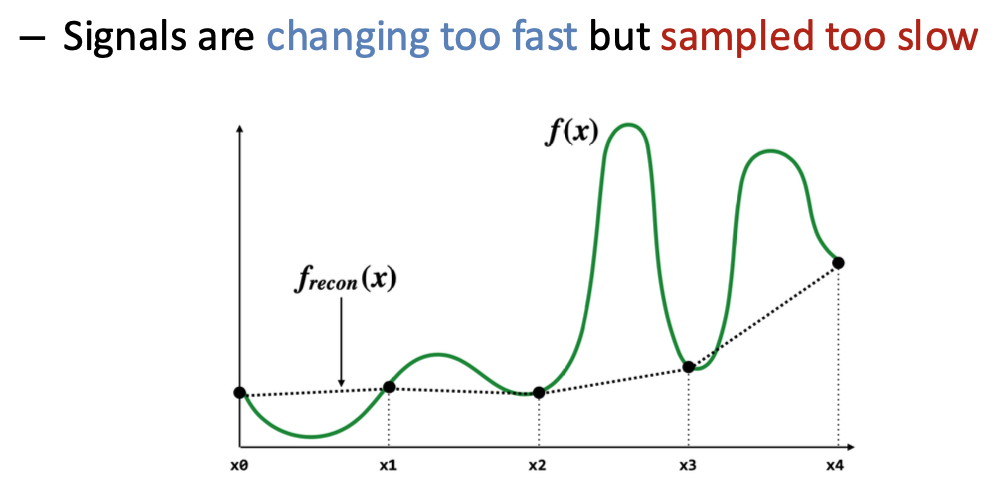
可能造成的情况
- 摩尔纹 (Moiré patterns)

- 车轮错觉 (wagon wheel illusion)
对于不同频率的信号使用相同采样率的结果:
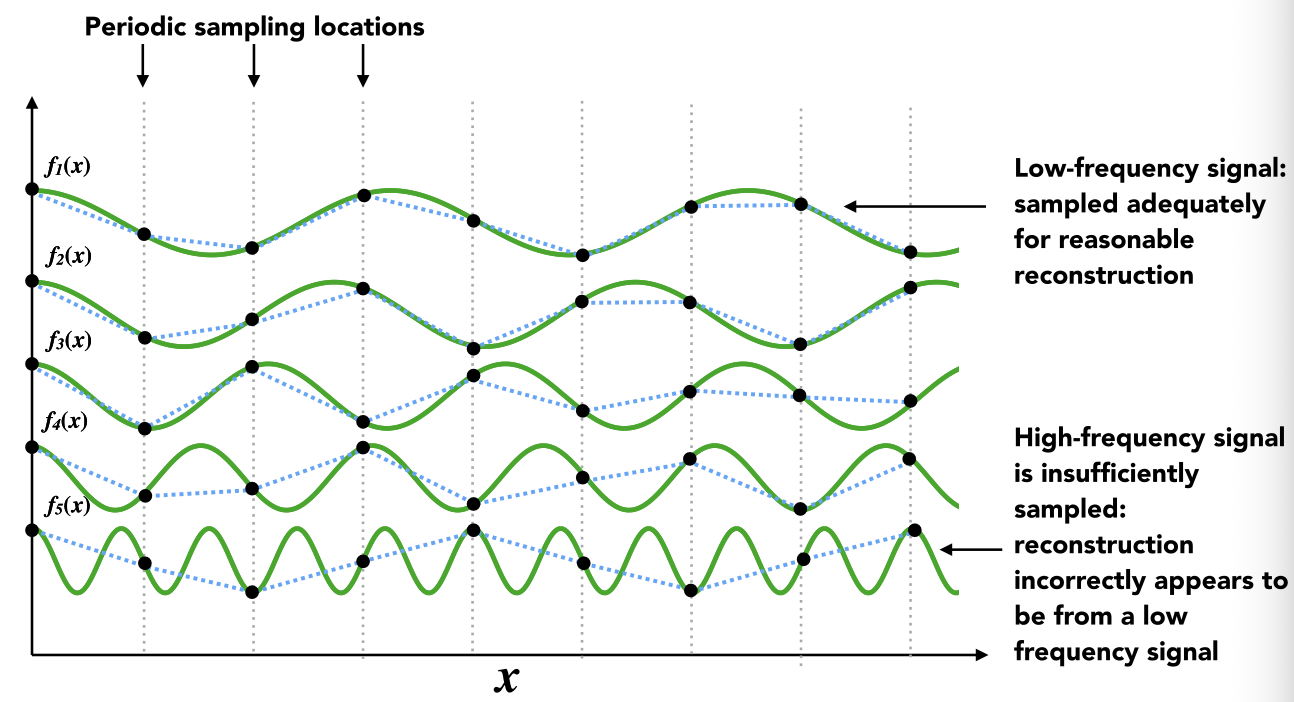
傅立叶变换 Fourier Transform
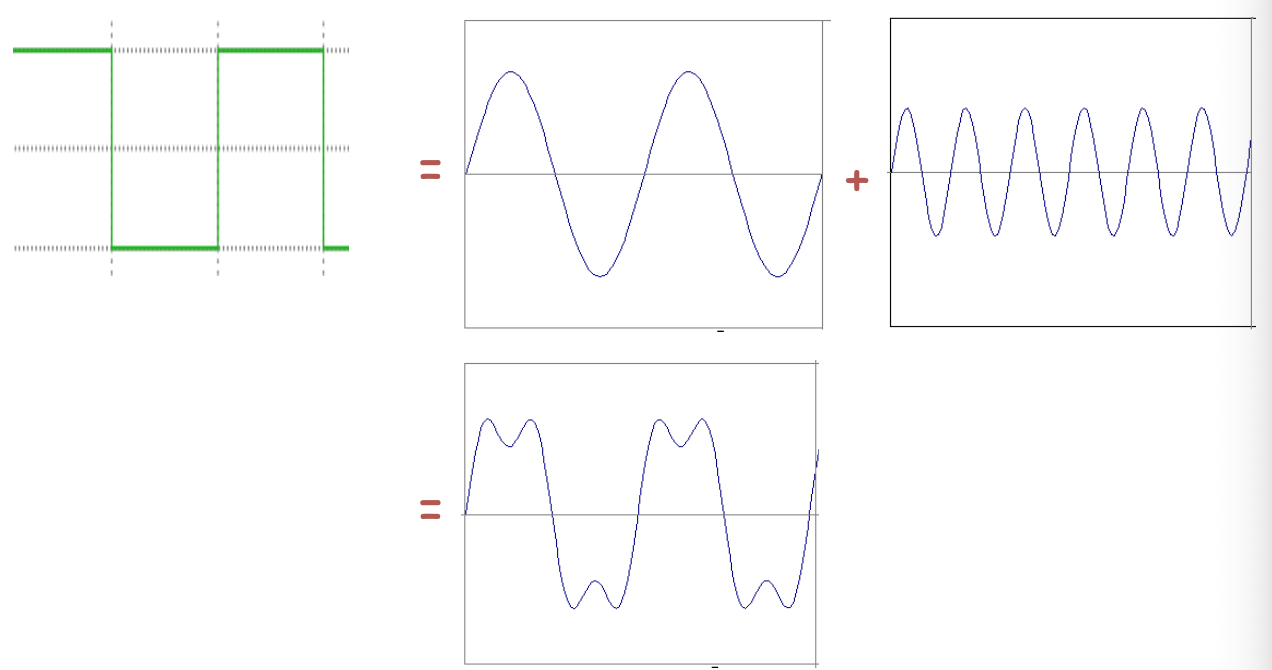
将一个信号表示为一组正弦/余弦函数的加权求和 (线性组合),其中的权重能够表示该频率在原有信号中所占的比例
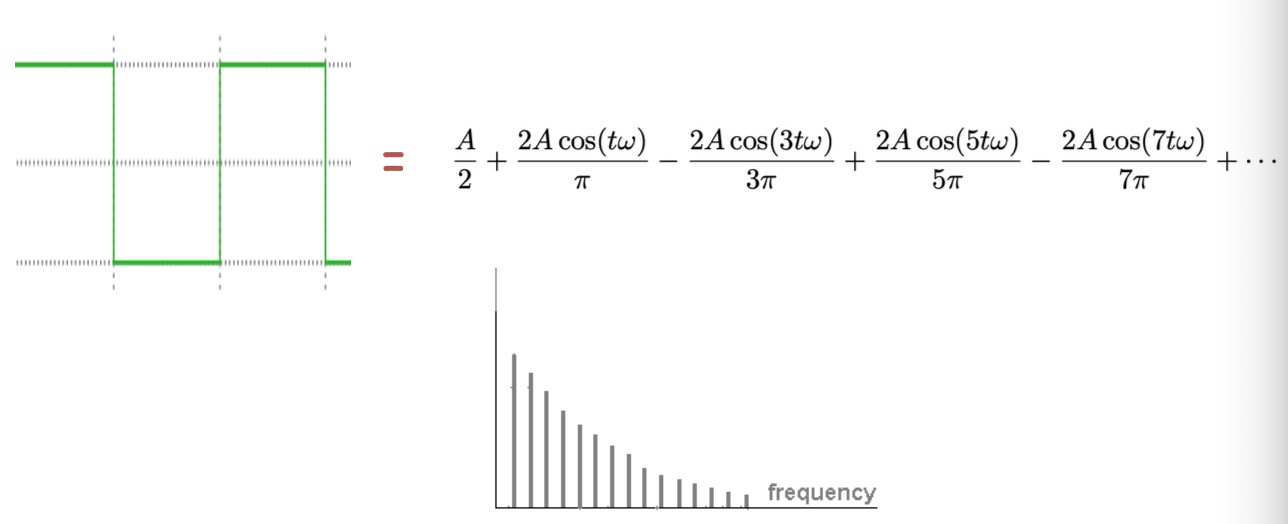
将其中的权重绘制成上图所示的直方图,即为该信号的频谱
正向变换:
根据欧拉公式:
其中的
逆向变换:
可以理解为通过加权求和将频谱还原为原来的信号
卷积定理
空间域中两个信号的卷积等价于频域中两个信号的乘积;同理,空间域中两个信号的乘积等价于频域中两个信号的卷积

图中频域的
由此可得,卷积操作也可以通过傅立叶变换后由成绩操作实现
二维傅立叶变换

上图表示二维的图片经过傅立叶变换得到的频谱
右图中心表示频率低的信号,由中心向四周,频率逐渐增大,其中水平和竖直方向的坐标分别表示各自方向上的频率
二维卷积定理
示例图:

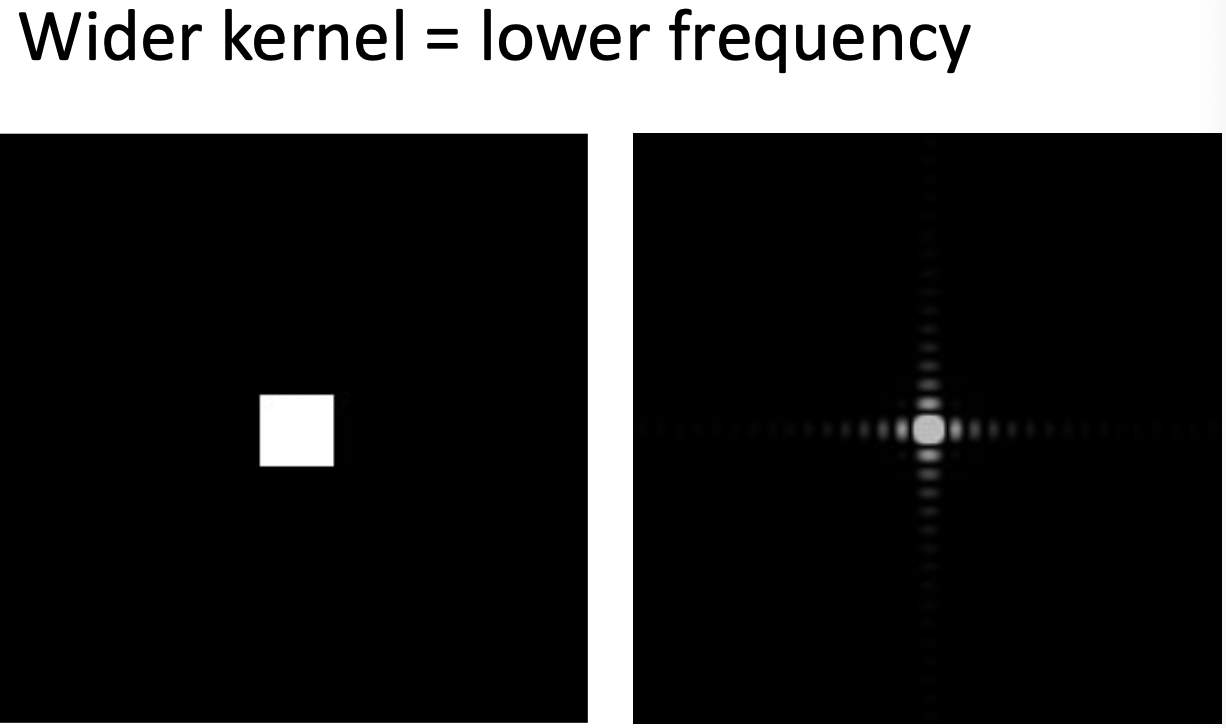
频域中二者的直接相乘可以直观的看出,中心的低频部分被保留,而边缘的高频部分被去除,从而实现了 box bluring,这也是卷积被称为滤波的原因
均值滤波和高斯滤波都是低通滤波器 (low-pass filter)

卷积核越大,频域越窄
总结
采样信号等价于在空间域中将信号与采样函数 (周期脉冲函数/周期狄拉克函数 Dirac comb function) 相乘
其从空间域到频域到傅立叶变换如下图所示:
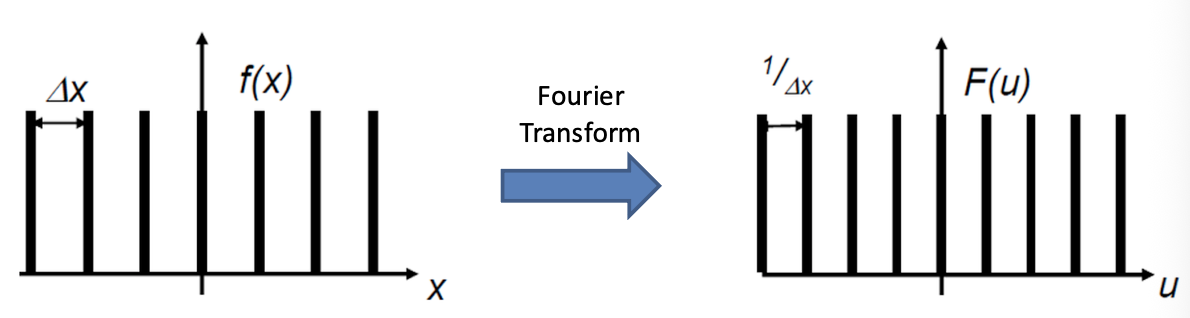
该函数在空间域的周期为
由此可得空间域与频域下的采样情况:
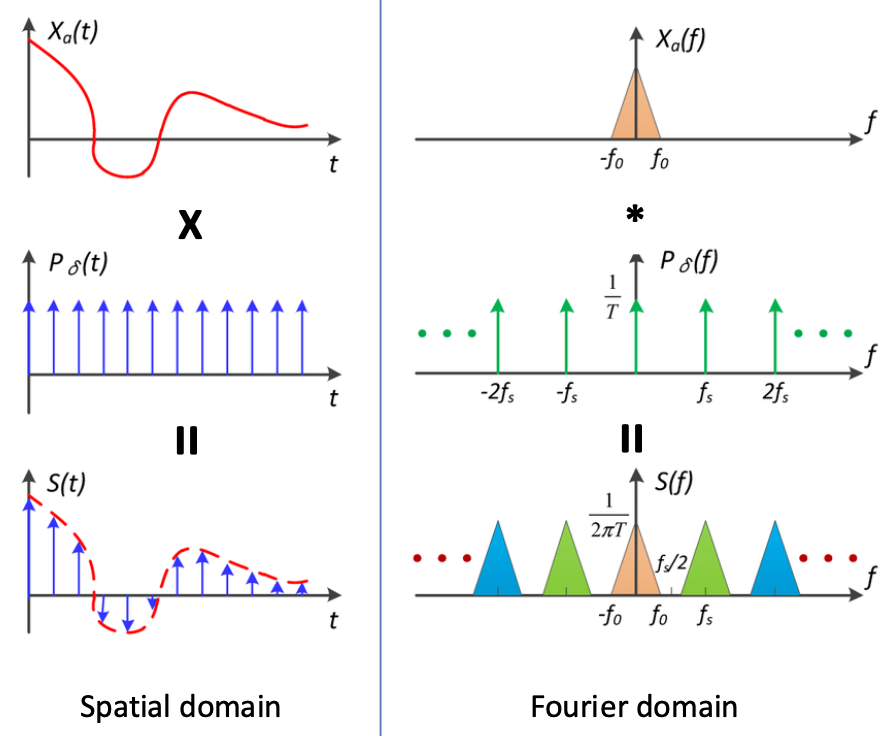
在采样频率足够大时,右图中采样得到的三角形不会重叠,若采样频率过小,则三角形会发生重叠,此时即发生了混叠 (aliasing),信号失真,无法通过采样后的信号还原原来信号的频谱,若要不发生失真,则
奈奎斯特-香农定理 Nyquist-Shannon theorem
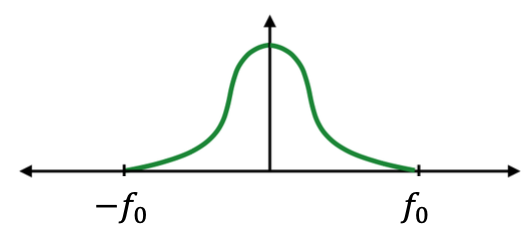
只有采样频率大于二倍信号频率 (
减少混叠
增加采样频率
Anti-aliasing
改变原来信号的频谱,在采样前使用低通滤波器减少一部分图像的高频部分
示例
可以通过 Anti-anliasing 减少锯齿和摩尔纹的出现
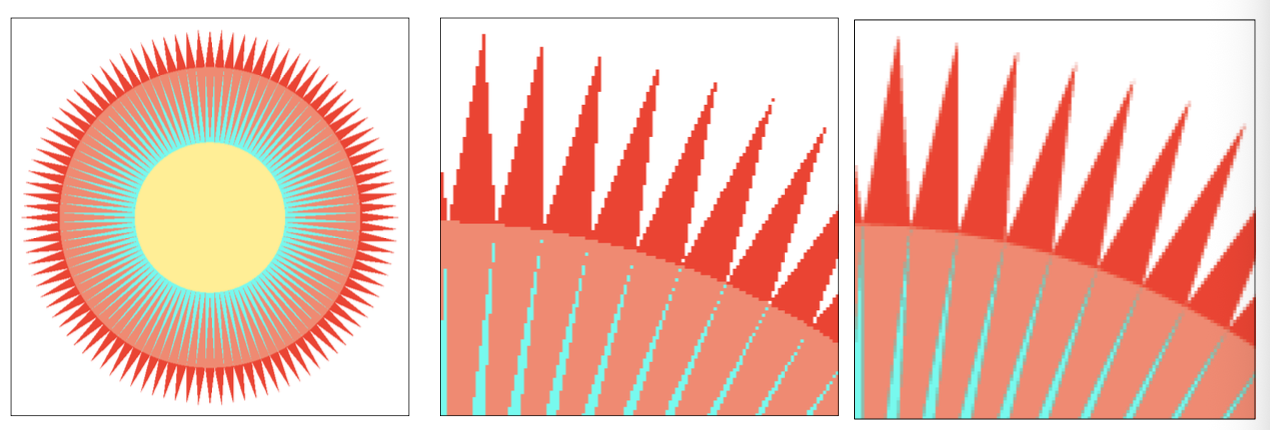

图像放大 Image magnification
上采样 Up sampling
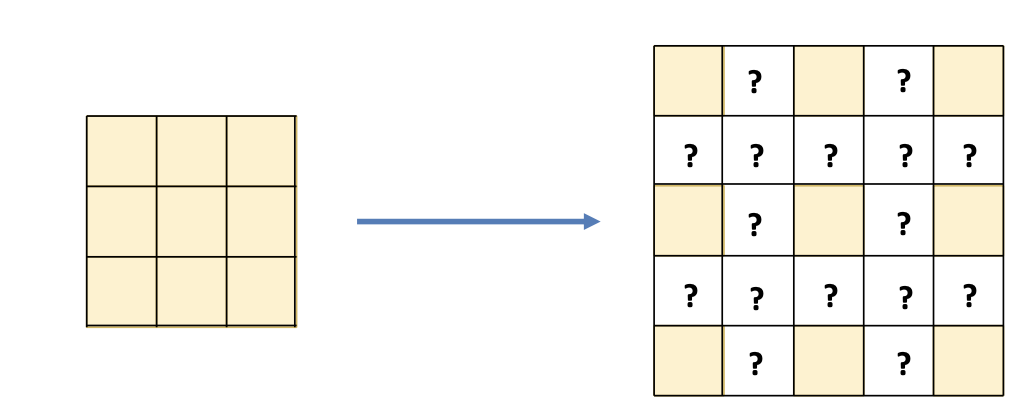
需要通过插值 (Interpolation) 来补充缺少的信息
插值 Interpolation
一维插值方法:
最近邻插值 Nearest-neighbor interpolation
得到的结果不连续、不光滑
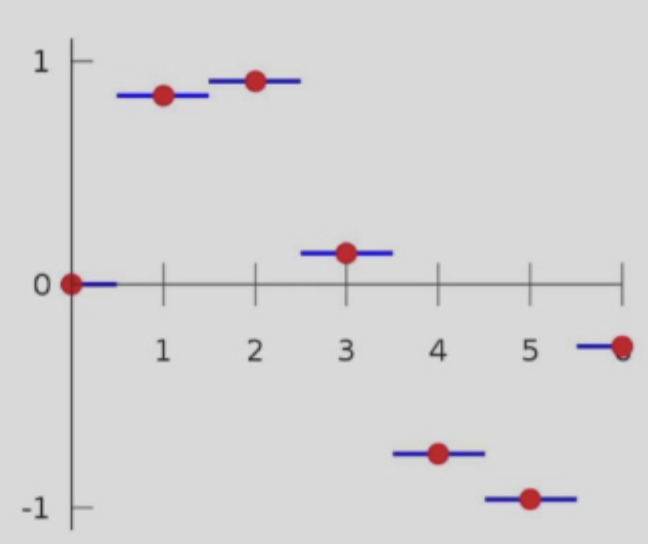
线性插值 Linear interpolation
得到的结果连续、不光滑
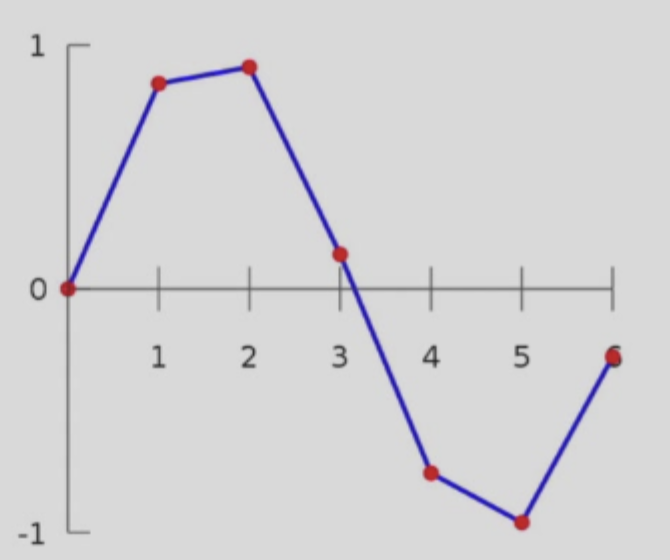
多项式插值 Cubic interpolation (三次多项式)
得到的结果连续、光滑
对每一段使用不同的多项式进行插值
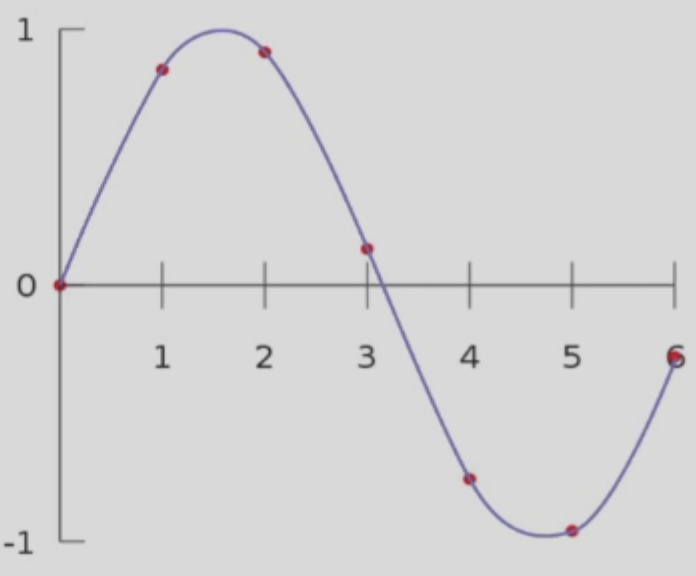
二维插值方法:
双线性插值 Bilinear interpolation
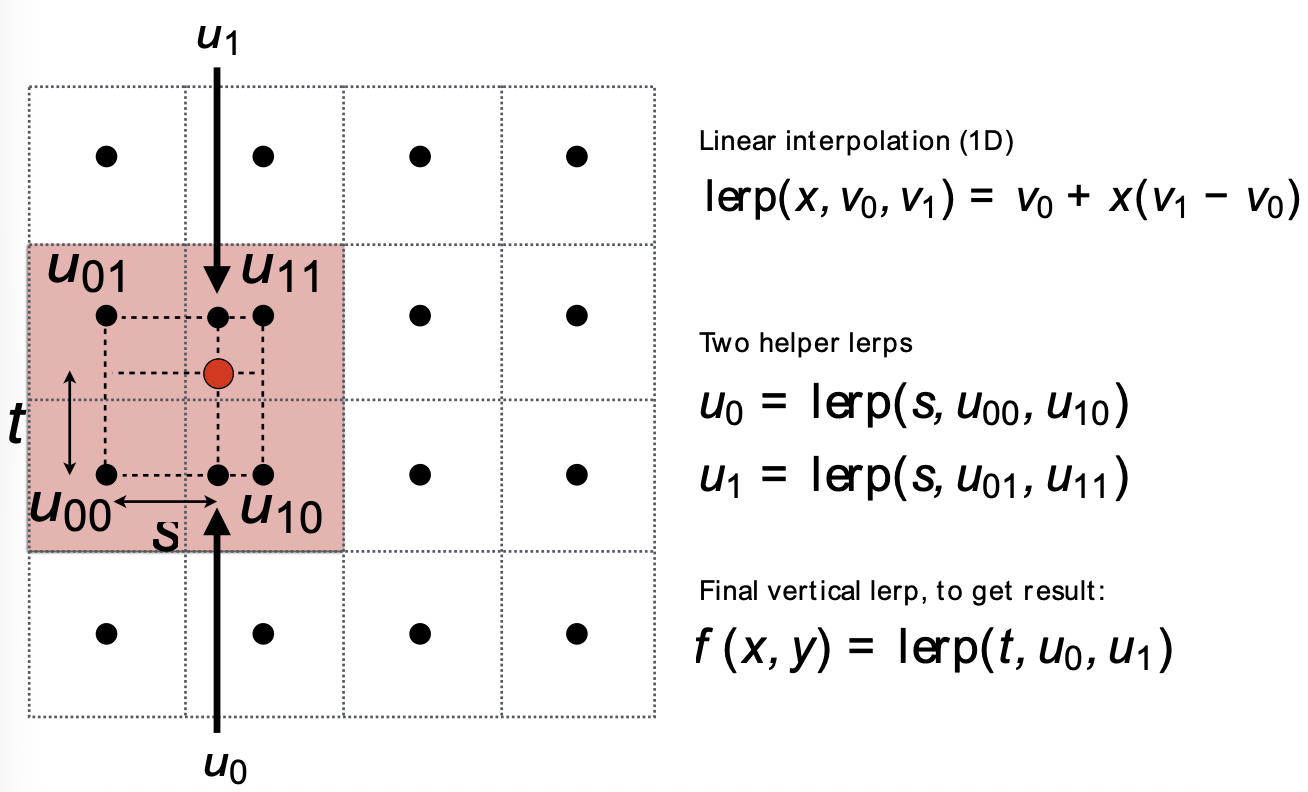
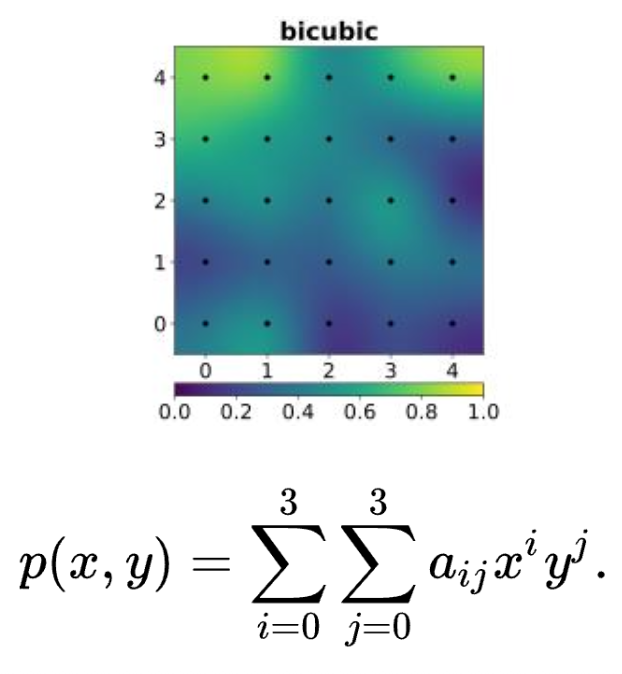
双多项式插值 Bicubic interpolation (三次多项式)
效果对比:
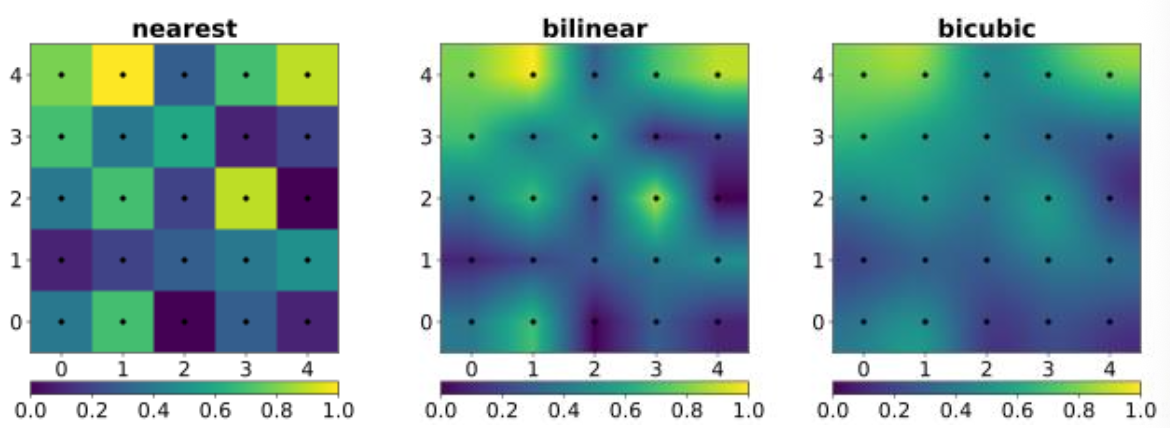
超分辨率 Super resolution
插值没有获得多余的信息,所以处理后仍然具有瑕疵,可以使用神经网络,通过超分辨率技术获得更多的信息,从而获得更好的效果
改变图像宽高比 Changing aspect ratio
直接压缩会导致画面内容发生畸变,直接剪切可能会导致画面中重要的信息丢失

可行的方案:
删去图片中不重要的部分 (与周围像素接近的部分)
使用边缘能量 (edge energy) 作为衡量指标:
通过卷积的方式进行求导,使用的卷积核为边缘检测卷积核
接缝裁剪 (seam carving):自顶向下寻找一条使像素边缘能量最小化的连接路径
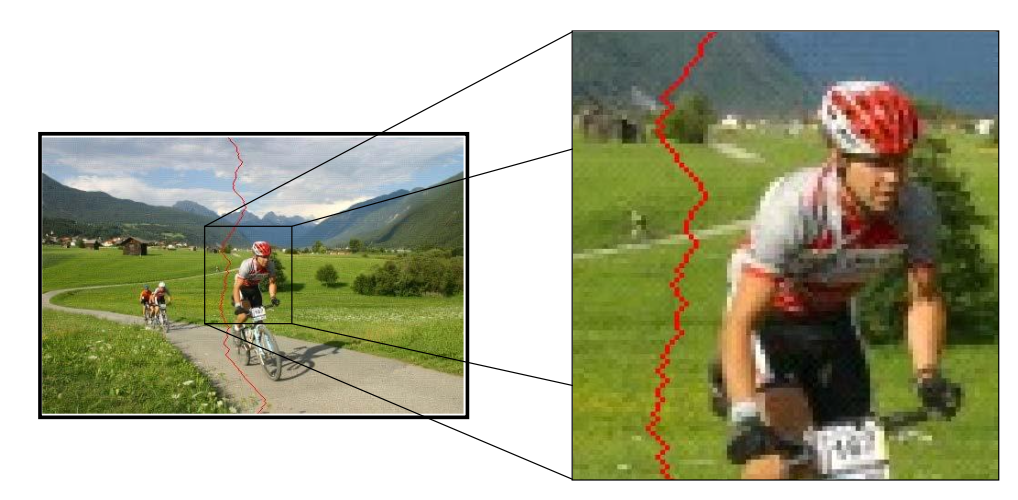
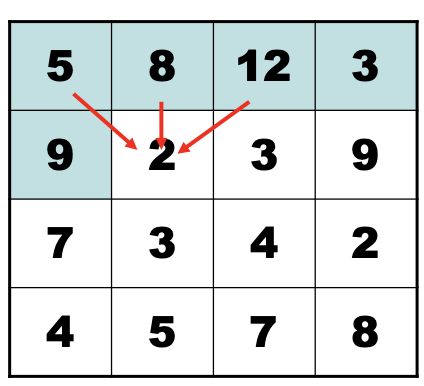
使用动态规划的最短路径思想求解
也可以通过接缝插入 (seam insertion) 来放大图像:

