线性代数与图像信息

线性代数 Linear Algebra

线性变换的几何意义

• Scale (缩放)

scale transform

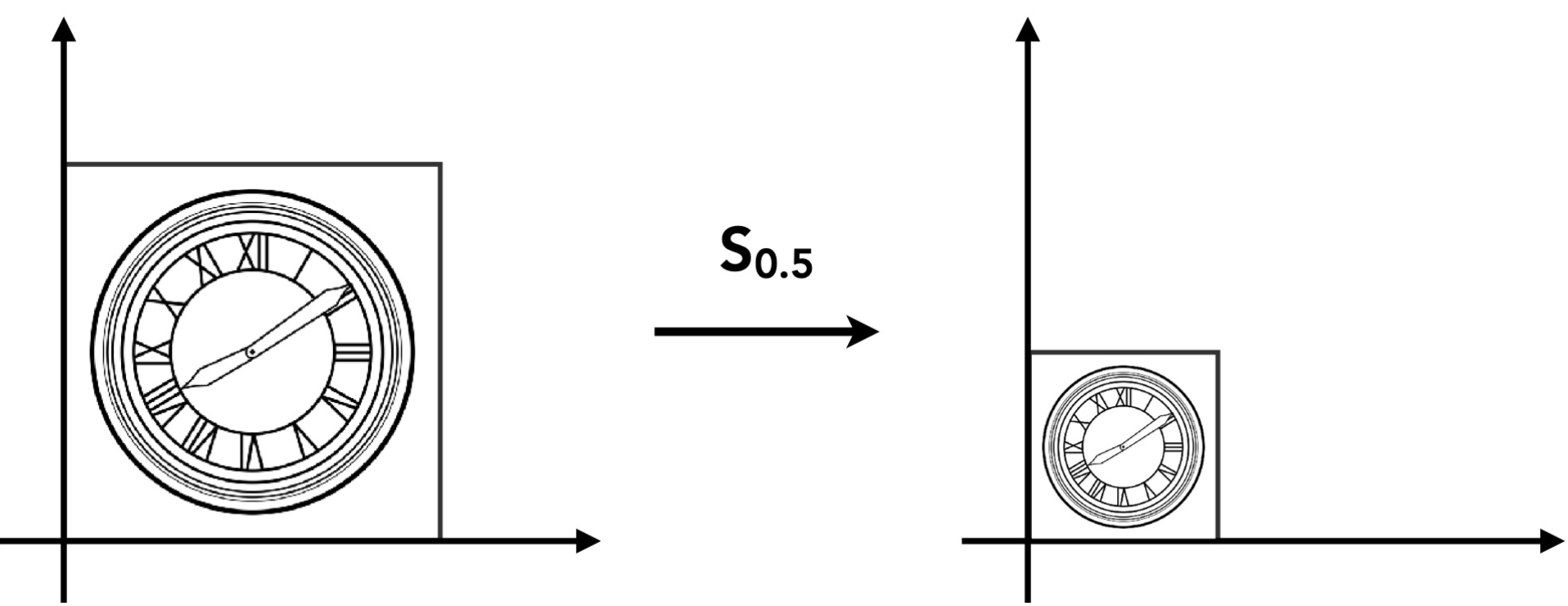
对于图中的变换，有：

$$\begin{array}{r}{x}^{\prime }=sx\\ y^{\prime }=sy\end{array}$$

写为矩阵形式：

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}s& 0\\ 0& s\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$$

• Reflection (镜像)

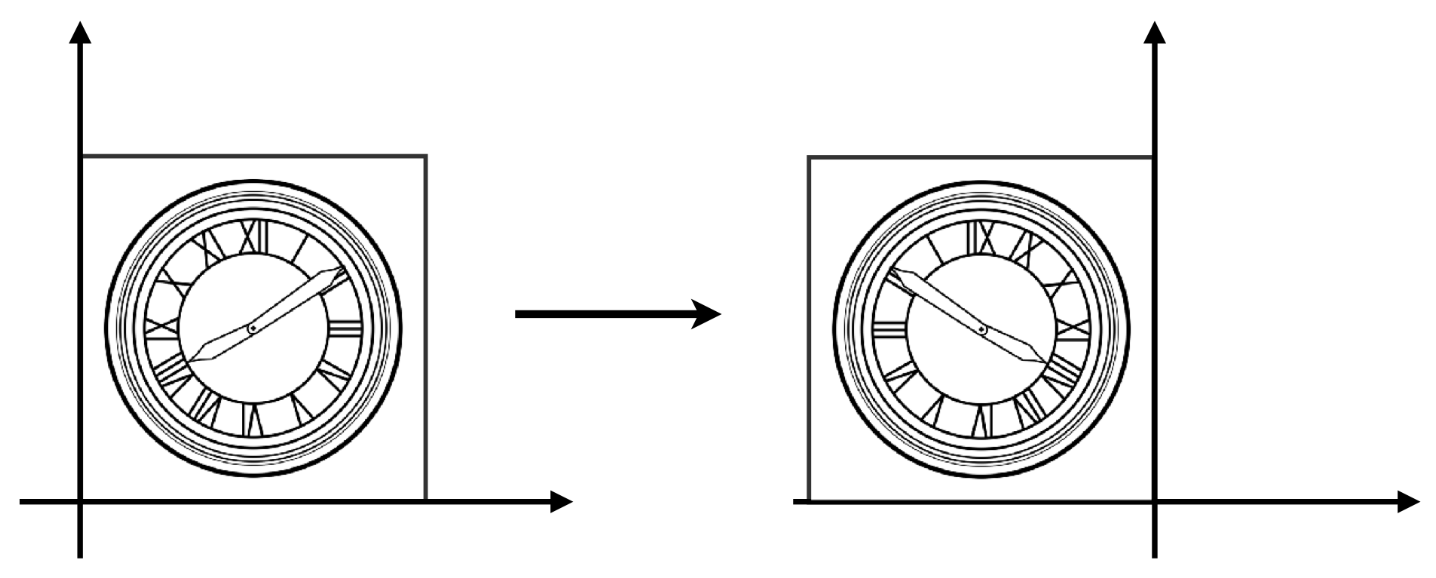
对于水平镜像：

$$x^{\prime }=-x$$$$y^{\prime }=y$$

转换为矩阵形式：

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$$

• Shear (剪切)

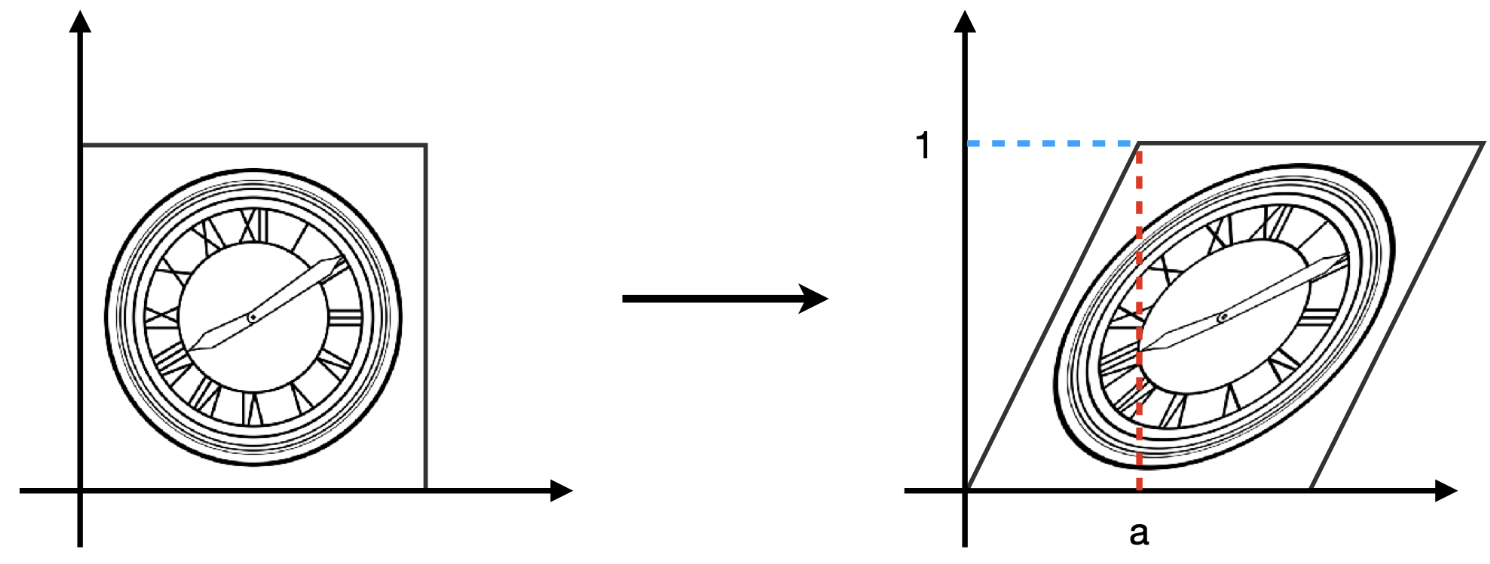
矩阵表示：

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}1& a\\ 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$$

• Rotation (旋转)

rotation transform

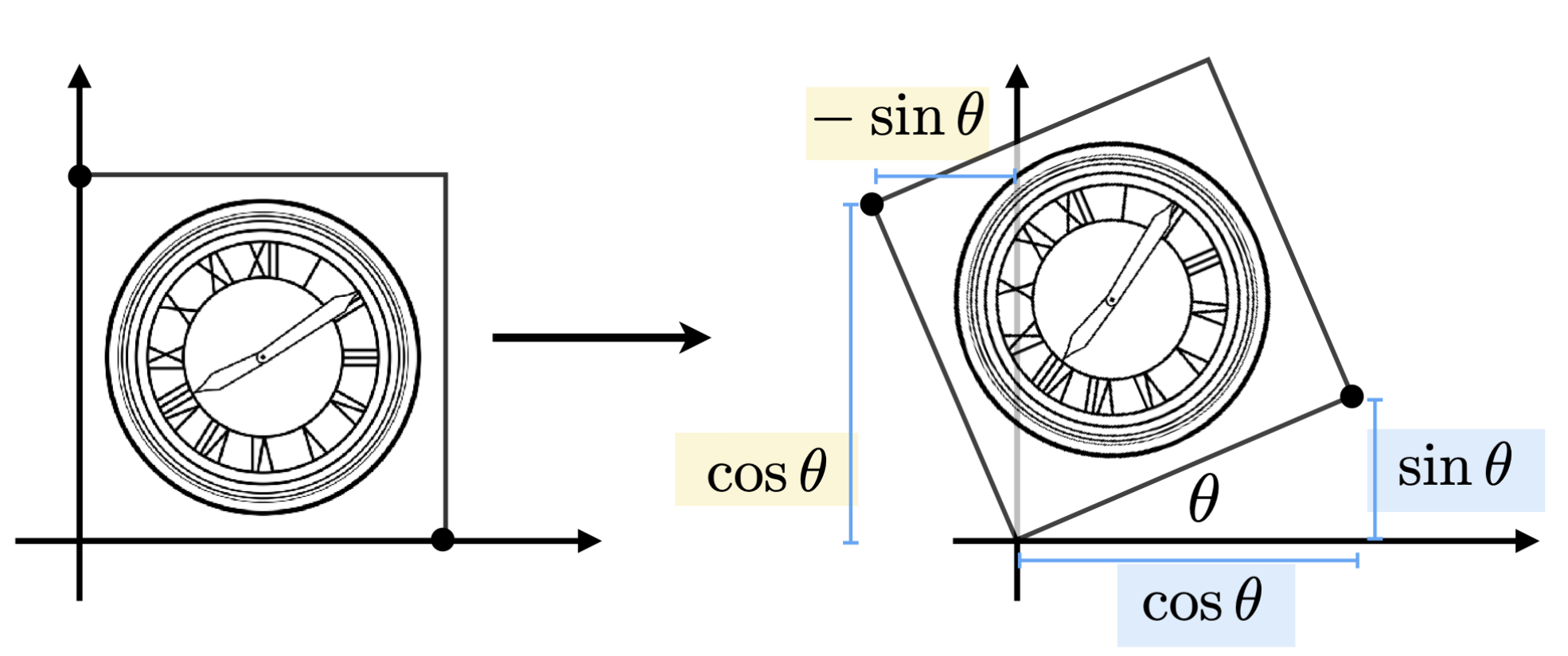
这一变换的矩阵表示为：

$$R_{\theta }=\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]$$

上述矩阵中的每一列可以看作原空间的基变换后的结果

即变换后的基为：$(\cos \theta ,\sin \theta ),(-\sin \theta ,\cos \theta )$

仿射变换 Affine Transformation

仿射变换 = 线性变换 + 平移

矩阵表示：

$$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)·\left(\begin{array}{c}x\\ y\end{array}\right)+\left(\begin{array}{c}{t}_x\\ t_y\end{array}\right)$$

笛卡尔坐标系下的仿射变换可以转化为齐次坐标系下的线性变换

矩阵表达如下：

$$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ 1\end{array}\right)=\left(\begin{array}{ccc}a& b& t_x\\ c& d& t_y\\ 0& 0& 1\end{array}\right)·\left(\begin{array}{c}x\\ y\\ 1\end{array}\right)$$

齐次坐标

关于齐次坐标的内容请参考下文齐次坐标

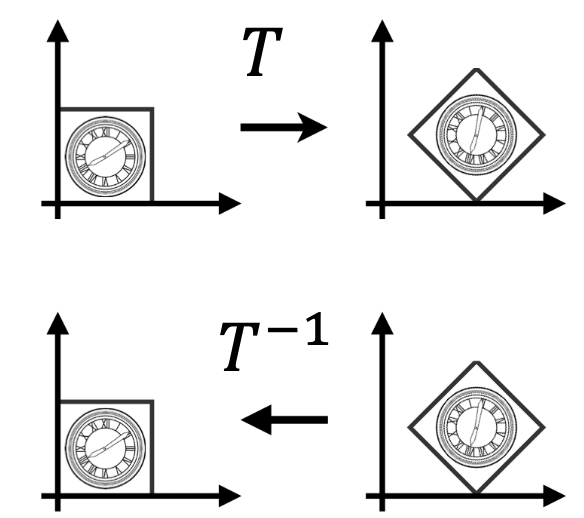
逆变换 Inverse Transform

$$T^{-1}$$

从矩阵角度和几何角度来看，$T^{-1}$ 是 $T$ 的逆变换

图像信息 Image Information

图像是三维空间的信息在二维空间的映射

相机和镜头 Camera and Lens

成像 Image Formation

直接将底片放在物体前无法形成清晰的像，因为此时底片上的一个点会接收到空间中多个点发出的光线，一般来说，只有当图像中的点与物理空间中的点是一一对应的，我们认为这个图像是清晰的

由此，我们引入了 Pinhole Camera Model

小孔相机 Pinhole Camera

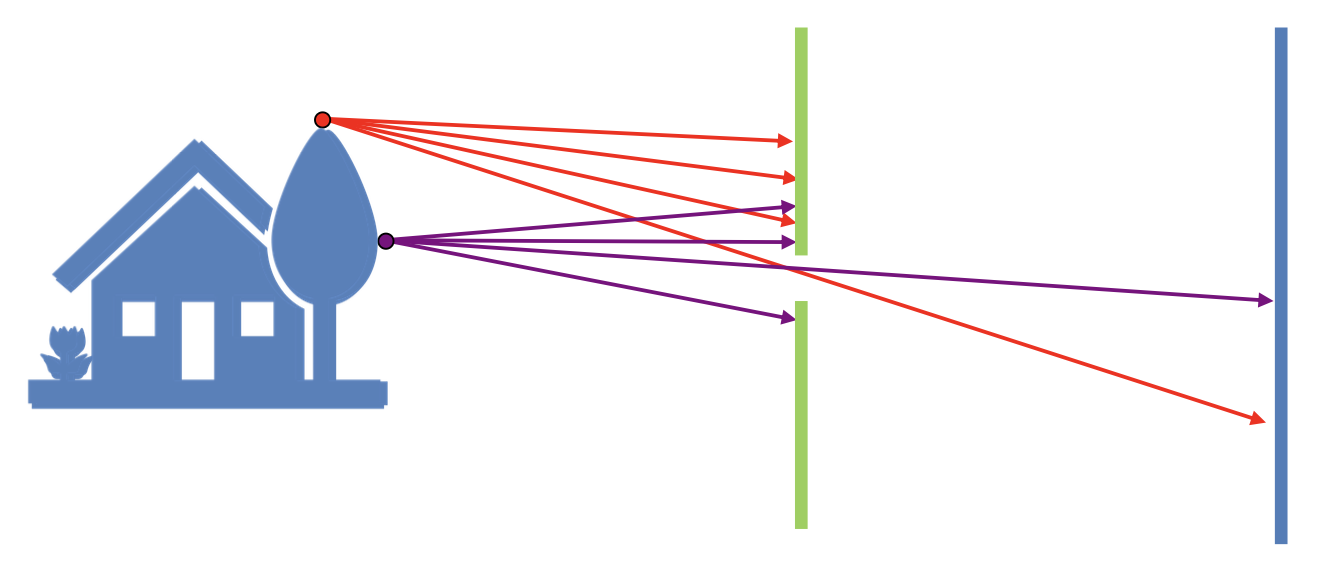
其中的隔板可以遮挡大部分光线，中间的小孔叫做光圈 (aperture)

在一定的范围内缩小光圈，可以使图像更清晰，但光圈过小时，会对图像的清晰度产生负面影响，原因为：

• 进光量减小

• 光的衍射

为了解决小孔相机对进光量的影响，我们引入了透镜

镜头 Lens

凸透镜有着和小孔一样的投影效果，但透镜能够聚集光线

高斯公式

$$\frac{1}{i}+\frac{1}{o}=\frac{1}{f}$$

i 表示像距，o 表示物距，f 表示焦距

变焦

包括物理变焦和数码变焦：

• 物理变焦：

  镜头组通过调整透镜来实现改变整体焦距的效果；或直接切换不同的镜头

• 数码变焦：

  镜头的物理焦距没有发生变化，仅仅是通过软件算法实现图像放大

图像放大率 Image Magnification

$$Magnification=\frac{h_i}{h_o}=\frac{i}{o}$$

根据高斯公式，当 $o$ 远大于 $i$ 时 (生活中的大部分情况)，$f\approx i$，因此焦距越大，图像的放大率越大

视场角 Field of View

在光学仪器中，以光学仪器的镜头为顶点，以被测目标的物像可通过镜头的最大范围的两条边缘构成的夹角，称为视场角

视场角

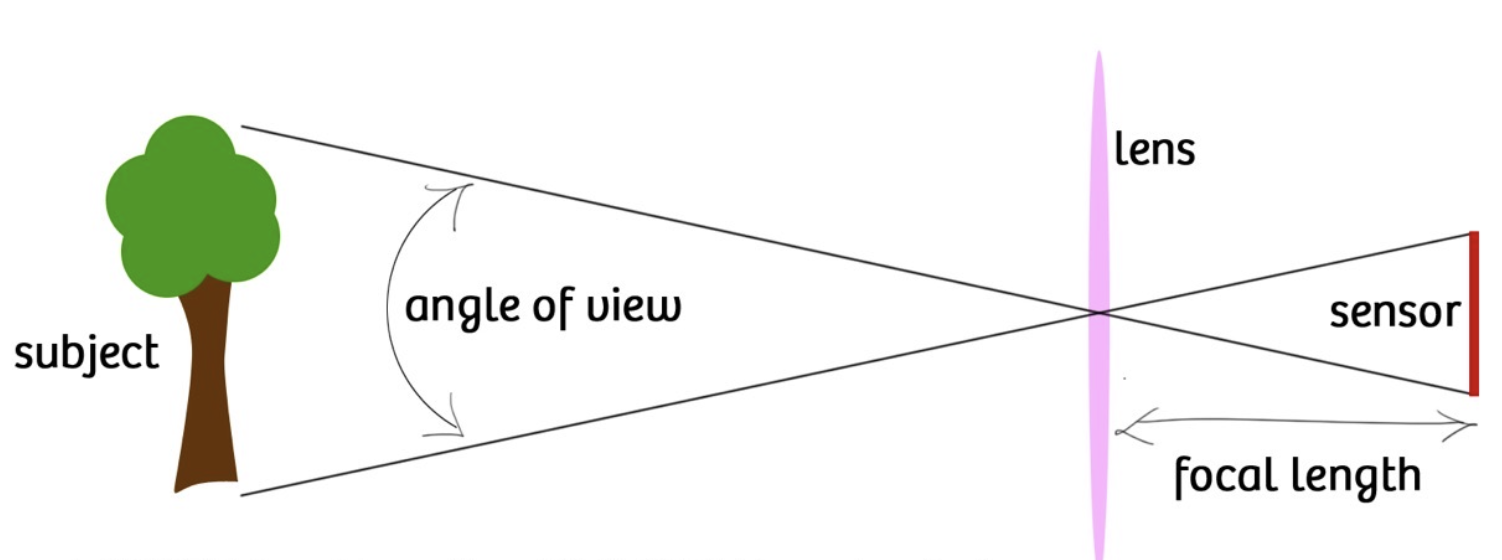
影响因素：

• 焦距 (focal length)

  焦距越长，放大率越大，视场角越小

  焦距越短，放大率越小，视场角越大

• 传感器大小 (sensor size)

  传感器越大，视场角越大

因此，图像的视野取决于传感器大小和焦距的比例

等效焦距

根据传感器的大小归一化后的焦距

光圈 Aperture

镜头的通光区域，通过调整光圈的大小来调整进光量，用镜头的直径来表示，记为D

进光量

进光量不仅可以通过调整光圈大小来控制，也可以通过调整快门时间来控制

F-Number

F 数可以通过如下公式计算：

$$N=\frac{f}{D}$$

镜头失焦 Lens Defocus

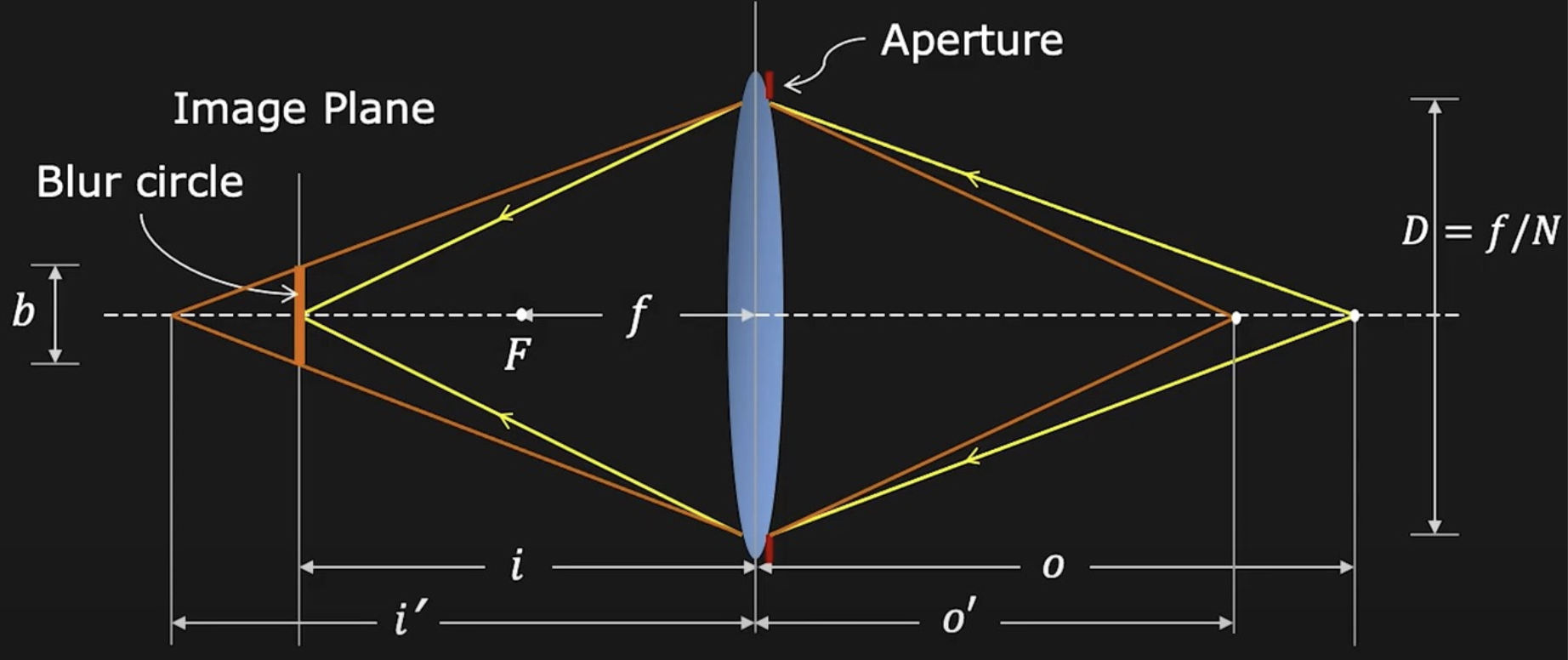
根据相似三角形，有：

$$\frac{b}{D}=\frac{|i^{\prime }-i|}{i^{\prime }}$$

因此光斑的大小可表示为：

$$b=\frac{D}{i^{\prime }}|i^{\prime }-i|,b\propto D\propto \frac{1}{N}$$

因此，减小光圈可以减小失焦形成的光斑大小

调焦 Focusing

在镜头和底片的位置确定的情况下 ($f$ 和 $i$ 确定时)，只有在同一垂直平面的物体成像是清楚的，因此，我们需要调焦

调焦的方法包括：调整像平面(image plane)和调整镜头的位置

调焦

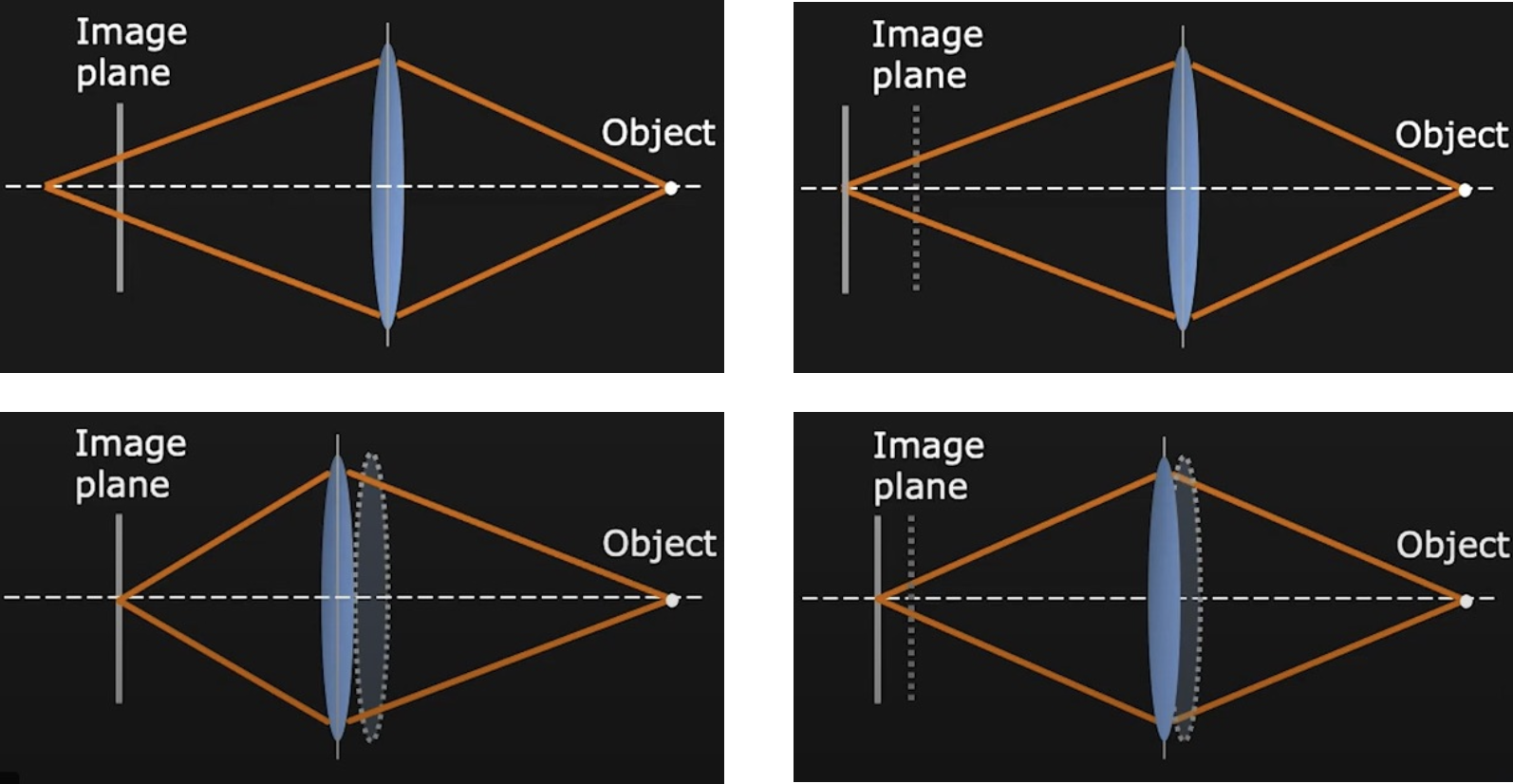
景深 Depth of Field

由于传感器的分辨率有限，在实际使用中，未必需要将像精准地聚焦到传感器上，只要光斑的直径b小于像素点的大小，就可以得到较为清晰的像

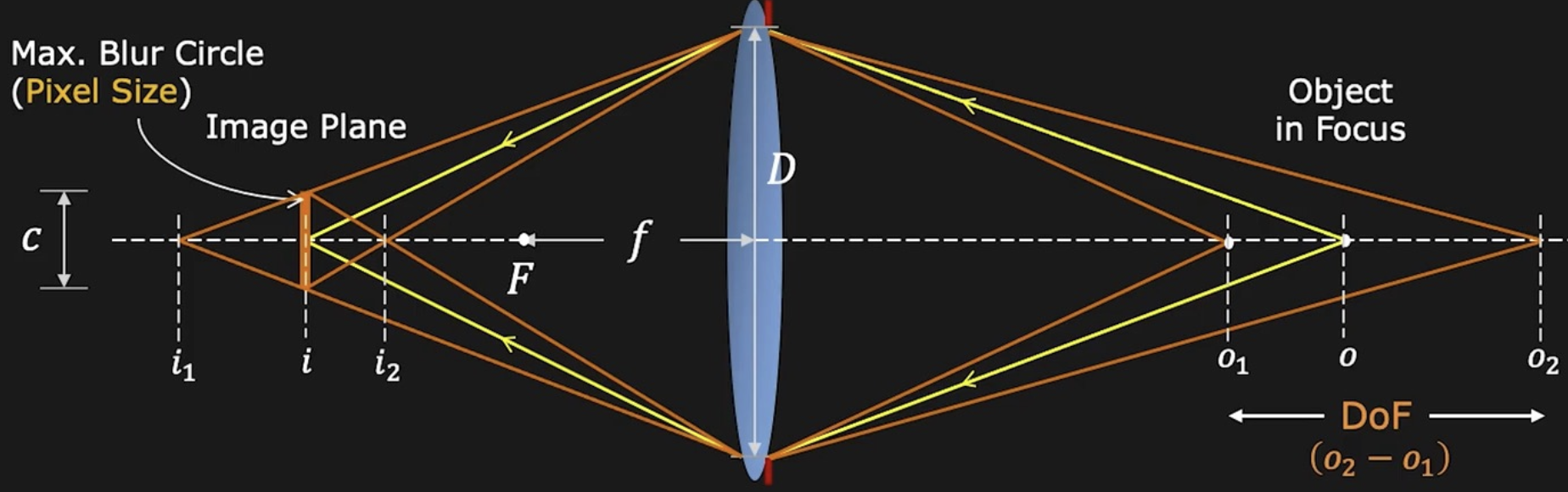
景深与焦距成反比，因此在拍摄人像时，可以选择更大的焦距，更容易地获得背景虚化的效果

可以通过如下方式来获得背景虚化的效果：

• Large aperture 更大的光圈

• Long focal length 更大的焦距

• Near foreground 更近的前景

• Far background 更远的背景

景深公式 (无需记忆)

$$\begin{array}{rl}c& =\frac{f^2(o-o_1)}{N{o}_1(o-f)}\\ c& =\frac{f^2(o_2-o)}{N{o}_2(o-f)}\\ o_2-o_1& =\frac{2o{f}^{2}cN(o-f)}{f^4-c^2{N}^2(o-f{)}^2}\end{array}$$

几何成像 Geometric image formation

3D 到 2D 空间的投影/几何变换

齐次坐标 Homogeneous coordinates

Pin-hole camera model: Perspective Projection

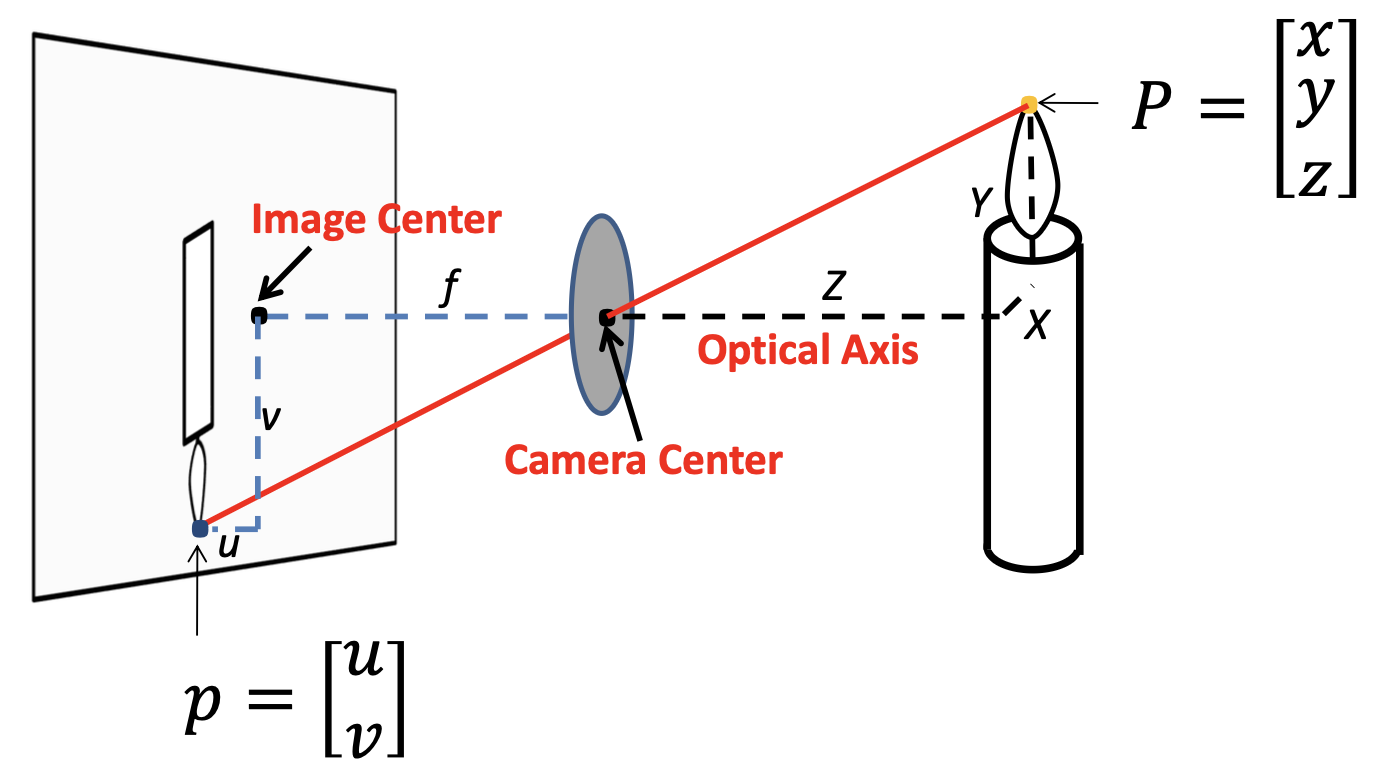
其中对坐标系的定义为：

三维空间中：镜头的中心位坐标系的原点，水平方向为 $x$ 轴，竖直方向为 $y$ 轴，平行于光轴的方向为 $z$ 轴

二维图像：图像中心 (光轴与像平面的交点) 为原点，水平方向为 $u$ 轴，竖直方向为 $v$ 轴

此处应用像距约等于焦距，从而有 $o\approx f$ (图片中 $f$ 的来源)

图中 $z$ 表示深度

由相似可以得到

$$p=\left[\begin{array}{c}u\\ v\end{array}\right]=\left[\begin{array}{c}\frac{fx}{z}\\ \frac{fy}{z}\end{array}\right]$$

可以看出，在笛卡尔坐标系中，这种投影变换不是线性的

由此引入齐次坐标，将这种投影运算转变为线性运算

笛卡尔坐标转化为齐次坐标

$$\begin{array}{rl}(x,y)& \to \left[\begin{array}{c}x\\ y\\ 1\end{array}\right]\\ (x,y,z)& \to \left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]\end{array}$$

齐次坐标转化为笛卡尔坐标

$$\begin{array}{rl}\left[\begin{array}{c}x\\ y\\ w\end{array}\right]& =\left[\begin{array}{c}\frac{x}{w}\\ \frac{y}{w}\end{array}\right]\\ \left[\begin{array}{c}x\\ y\\ z\\ w\end{array}\right]& =\left[\begin{array}{c}\frac{x}{w}\\ \frac{y}{w}\\ \frac{z}{w}\end{array}\right]\end{array}$$

注意

齐次坐标是缩放不变的

一个齐次坐标可能对应多个笛卡尔坐标，但它们只有长度上的缩放关系

齐次坐标中的透视投影

在齐次坐标系中，透视投影可通过线形运算表示，公式如下：

透视投影公式

$$\left[\begin{array}{cccc}f& 0& 0& 0\\ 0& f& 0& 0\\ 0& 0& 1& 0\end{array}\right]\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]=\left[\begin{array}{c}fx\\ fy\\ z\end{array}\right]=\left[\begin{array}{c}f\frac{x}{z}\\ f\frac{y}{z}\\ 1\end{array}\right]$$

上述公式中：$\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]$ 表示物体在齐次坐标系下的坐标，$\left[\begin{array}{c}fx\\ fy\\ z\end{array}\right]$ 表示像在齐次坐标系下的坐标，$\left[\begin{array}{c}f\frac{x}{z}\\ f\frac{y}{z}\\ 1\end{array}\right]$ 表示像在笛卡尔坐标系下的坐标

透视投影可视化

可以将像平面等效翻转到镜头前

透视投影 Perspective Projection

信息损失

经过透视投影后，由于物体相对于相机的深度信息损失，导致成像中长度、角度等信息会损失，但线的曲直(直线仍然是直的)等信息仍然得到保留

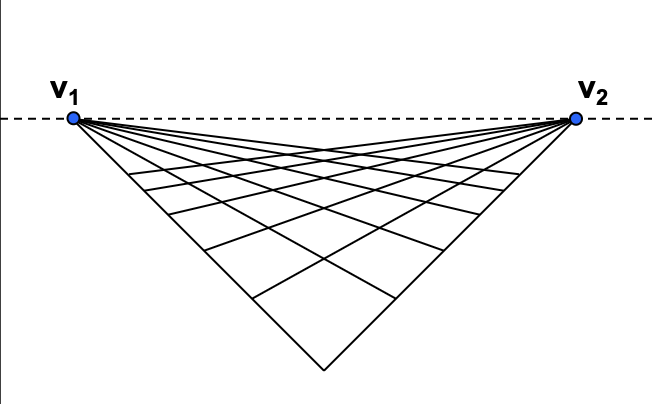
灭点 Vanishing Point

空间直线与成像平面不平行时，该直线在成像平面上的投影为收敛于灭点的线段

若空间直线垂直于成像平面，则灭点位于像平面中心

若一组平行线平行于成像平面，则它所成的像依旧平行，即灭点位于无穷远处

由此可以获得空间中的线相对于相机的位置

性质：

• 两条平行线有相同的灭点 v

• 相机中心与灭点连成的直线平行于原直线

• 灭点可能在画面外或无限远处

灭线 Vanishing Line

空间平面与成像平面不平行时，该平面在成像平面上的投影为收敛于灭线的区域，相互平行的空间平面在成像空间收敛于同一条灭线

垂直于成像平面的平面对应的灭线在画面中央

灭线与镜头中心所成的平面平行于该平面

该平面中所有直线的灭点都在这条灭线上

同理于灭点，通过灭线可以获得空间中的平面相对于相机的位置

透视畸变 Perspective Distortion

由透视投影的性质引起，与镜头无关

带来的现象有：

• converging verticals

示例

楼梯形变为梯形，平行线在图像中可相交

• 球体形变为椭圆

球心与镜头中心的连线不垂直于成像平面，且越偏离垂直状态，形变为椭圆的程度越严重

(球面上的各点与镜头中心的连线形成锥形结构，以不垂直于轴线方向切割该锥形，从而得到椭圆)

示例

径向畸变 Radial Distortion

径向畸变主要由镜头的缺陷引起，光线通过镜头边缘的成像更加明显

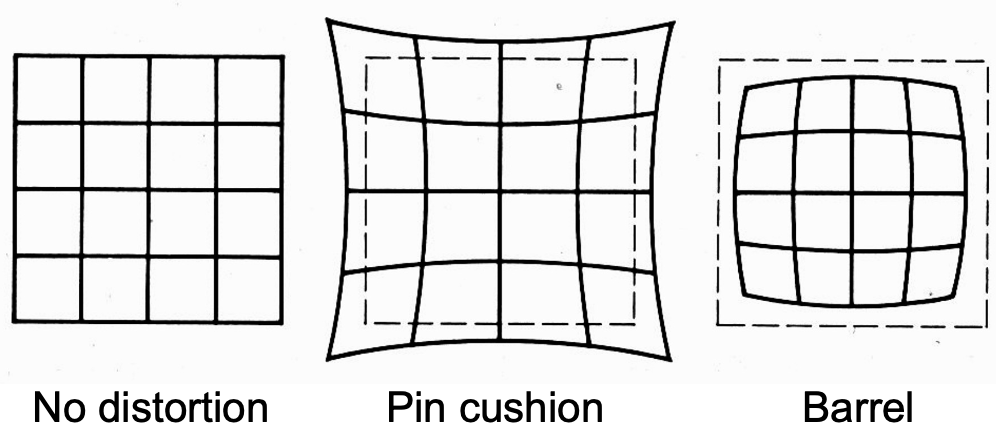
分为：

• 枕形畸变 Pin cushion

• 桶形畸变 Barrel

短焦 (广角)镜头更容易发生桶形畸变，长焦镜头更容易发生枕形畸变

由于发生了径向畸变，最终成像点的位置不完全符合透视投影中投影点的位置

$$\begin{array}{rl}{r}^2& ={x_n^{{}^{\prime }}}^2+{y_n^{{}^{\prime }}}^2\\ x_d^{{}^{\prime }}& =x_n^{{}^{\prime }}(1+{\kappa }_1{r}^2+{\kappa }_2{r}^4)\\ y_d^{{}^{\prime }}& =y_n^{{}^{\prime }}(1+{\kappa }_1{r}^2+{\kappa }_2{r}^4)\end{array}$$

$x_n^{{}^{\prime }}$ 和 $y_n^{{}^{\prime }}$ 是透视投影中投影点的位置，$x_d^{{}^{\prime }}$ 和 $y_d^{{}^{\prime }}$ 是发生径向畸变后投影点的位置

正交投影 Orthographic Projection

正交投影可以视为透视投影的特殊情况，当投影中心 (COP) 到投影 (PP) 平面的距离无穷大时，透视投影退化为正交投影

正交投影并没有近大远小的效果

正交投影公式：

$$\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]=\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]\to (x,y)$$

光度成像 Photometric Image Formation

描述了三维世界物理性质和二维图像的颜色之间的关系

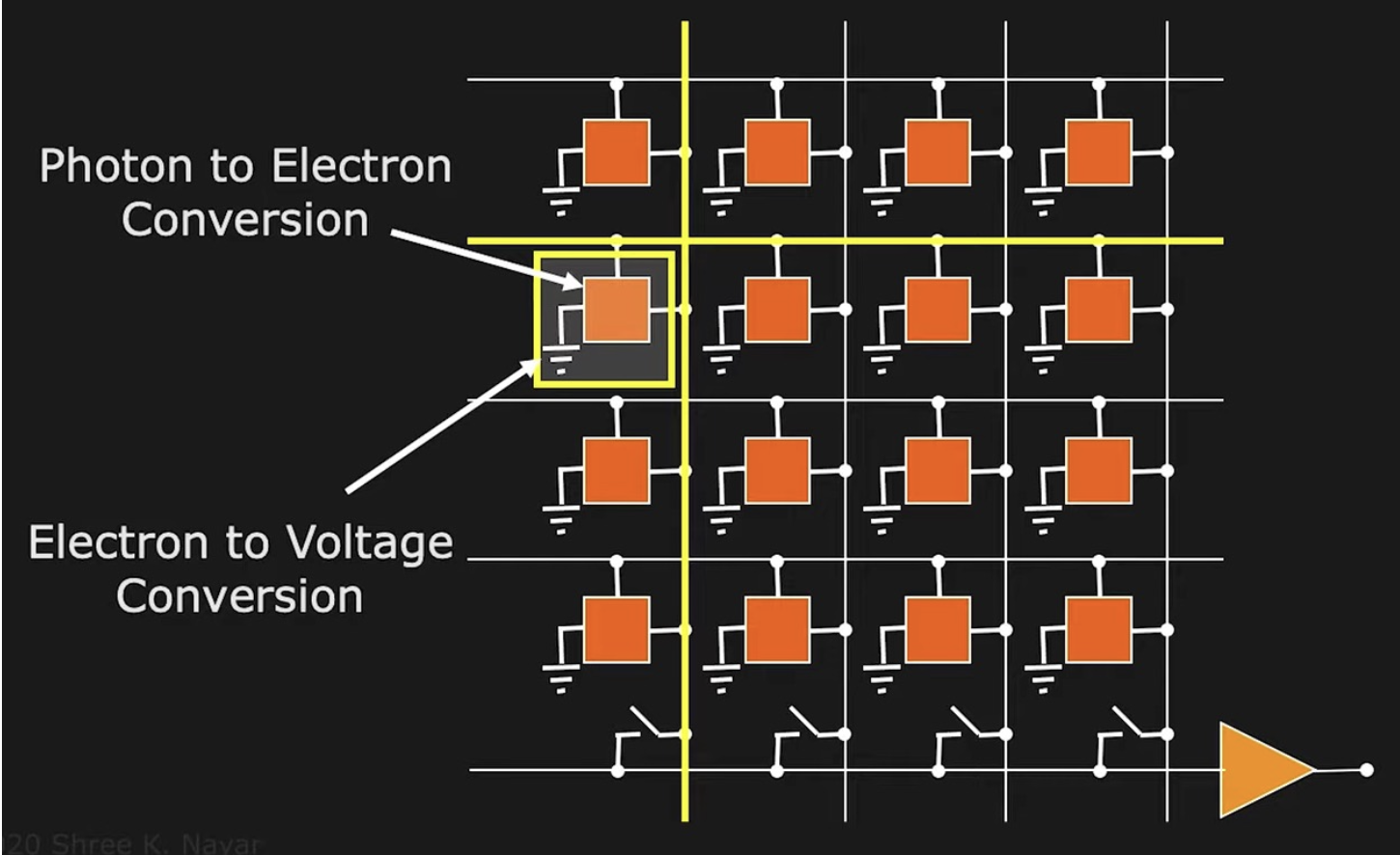
图像传感器

CMOS：光子 -> 电子 -> 电压

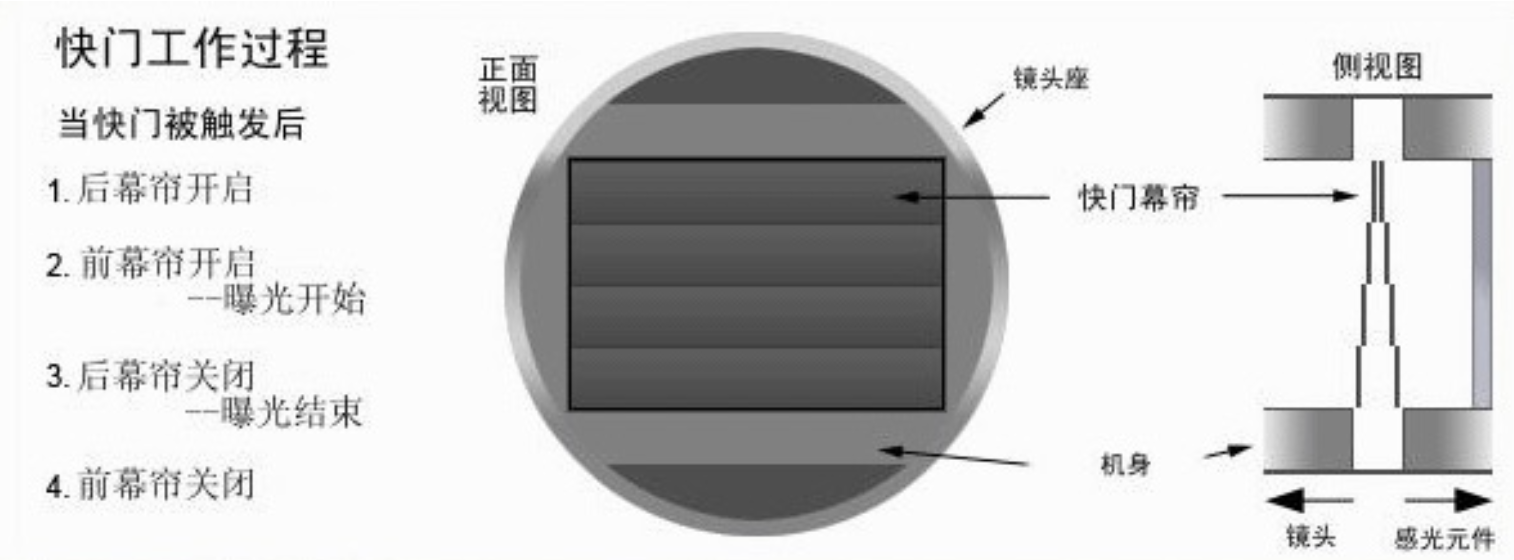
快门 Shutter

快门速度 Shutter speed

快门速度可以控制曝光时间，快门时间过短会导致成像过暗，快门时间过长易导致画面模糊 (相机或物体发生移动)

果冻效应 Rolling shutter effect

快门分为全局快门 (Global shutter) 和 卷帘快门 (Rolling shutter)

对于全局快门，整个传感器同时曝光；而卷帘快门的传感器使用逐行曝光

若卷帘快门进行曝光时，物体快速移动，就可能导致图像中的物体变形，发生果冻效应

色彩空间 Color space

物理世界中，我们使用波长来描述不同颜色的光

在计算机中，我们使用不同的色彩空间对颜色进行描述

• RGB 色彩空间

  红、绿、蓝三种颜色，每个颜色通过 0～255 8bit 的数据进行表示

  

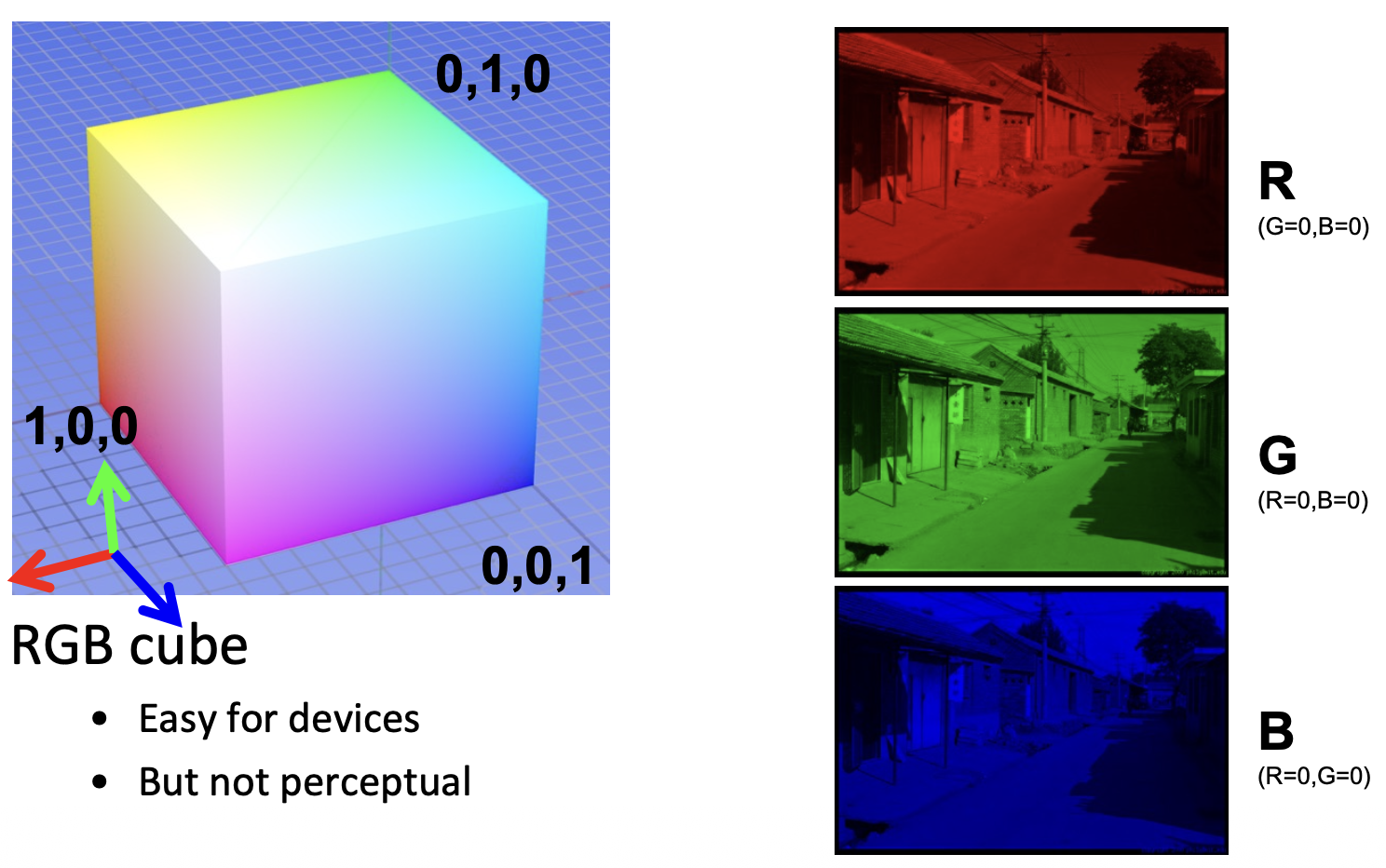
• HSV 色彩空间

  • H: Hue 色相 通过角度表示颜色的种类

  • S: Saturation 饱和度 颜色的纯度

  • V: Value 亮度 表示颜色的明暗程度

    

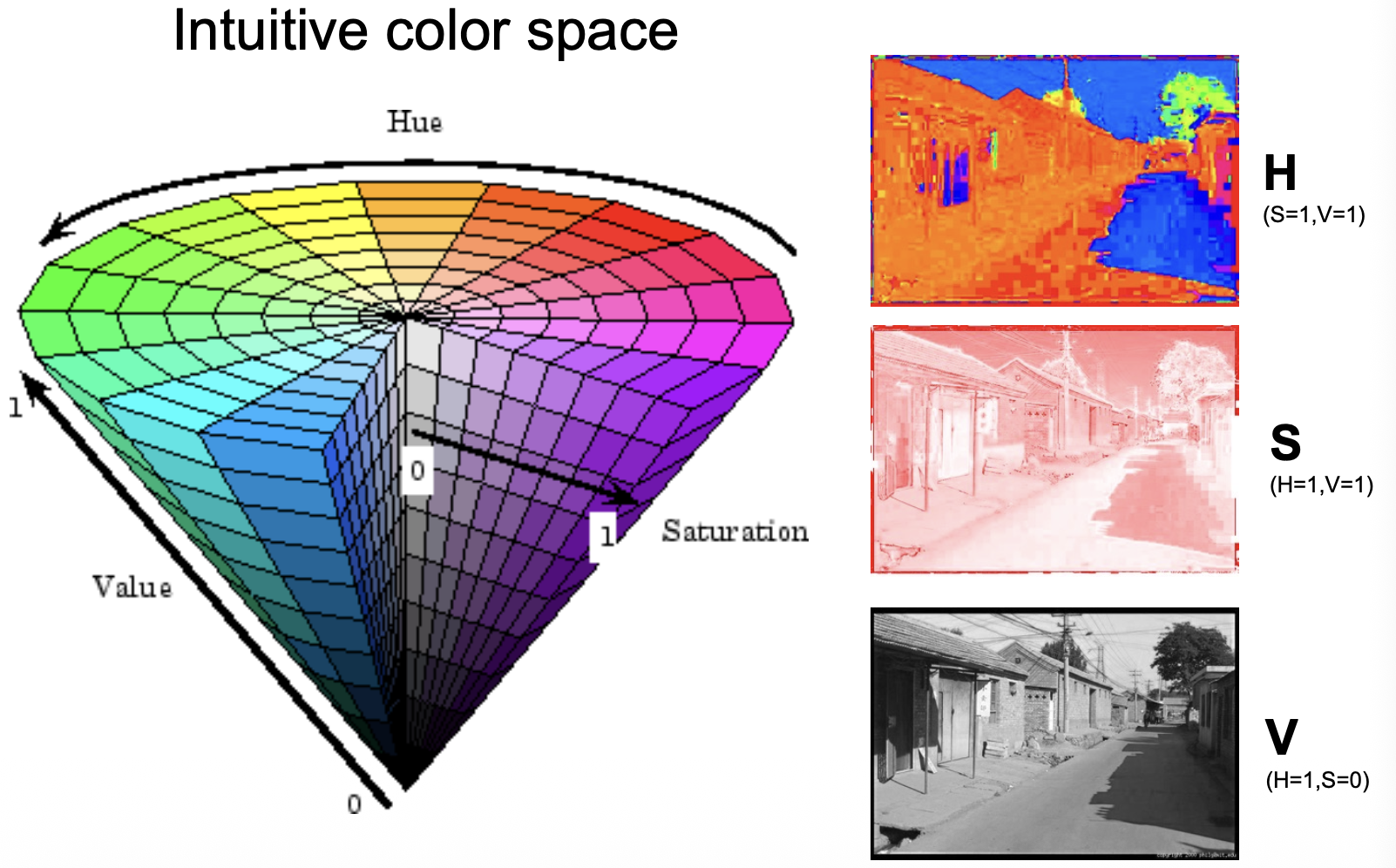
HSV 色彩空间和 RGB 色彩空间可以相互转换

图片的颜色数据在 python 中以三维矩阵的形式存在 (Height, Width, Channel)

颜色感知 Color Sense

使用拜耳滤镜 (Bayer filter) 来在单个芯片上记录光的颜色

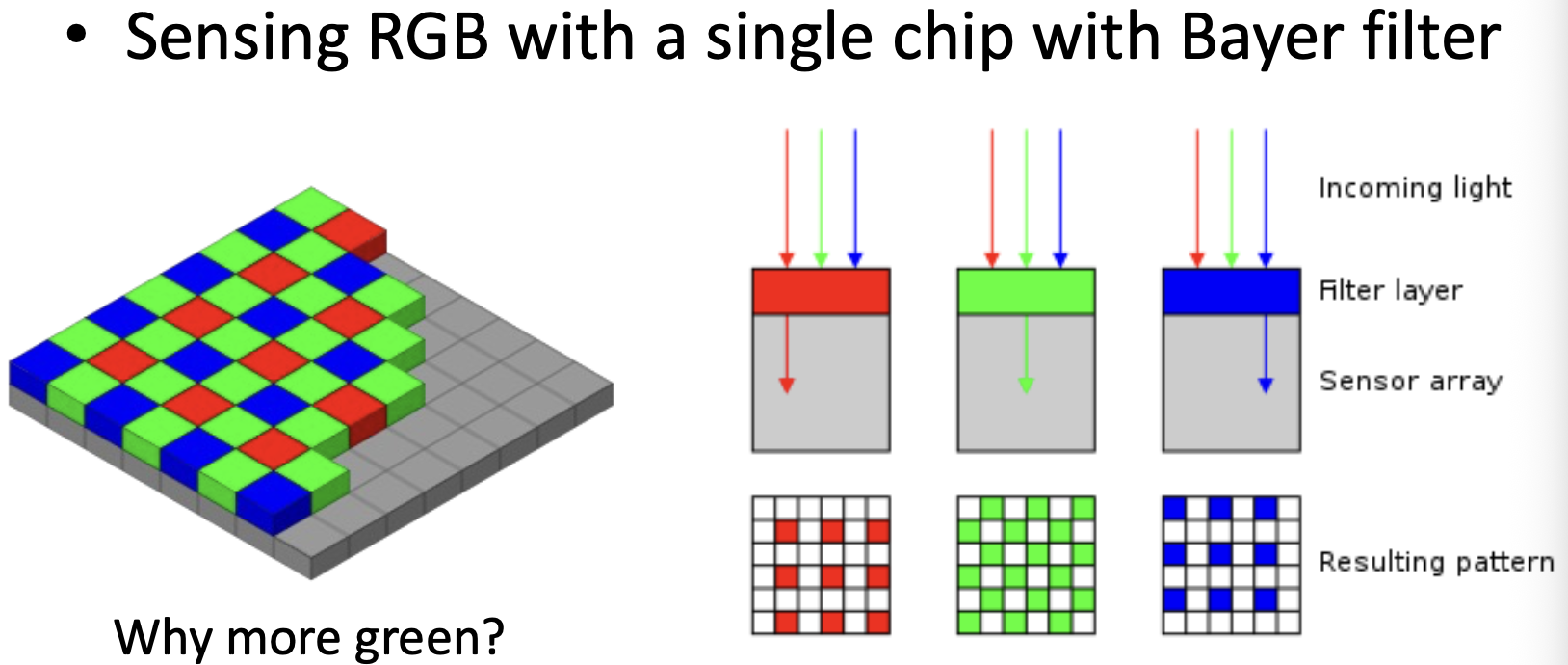
单个芯片智能记录一种颜色的光

四个芯片排列的方形结构记录一个完整的 RGB，绿色滤镜数量更多（人眼对绿色更加敏感）

由于四个芯片才能记录一个完整 RGB，会导致得到图像不连续，需要借助图片差值进行复原

着色

计算机图形学知识，简要了解即可

物体的颜色由物体物体表面反射/折射的光线决定，而这又与物体的材质相关

数学中通过 BDRF 描述物体的材质

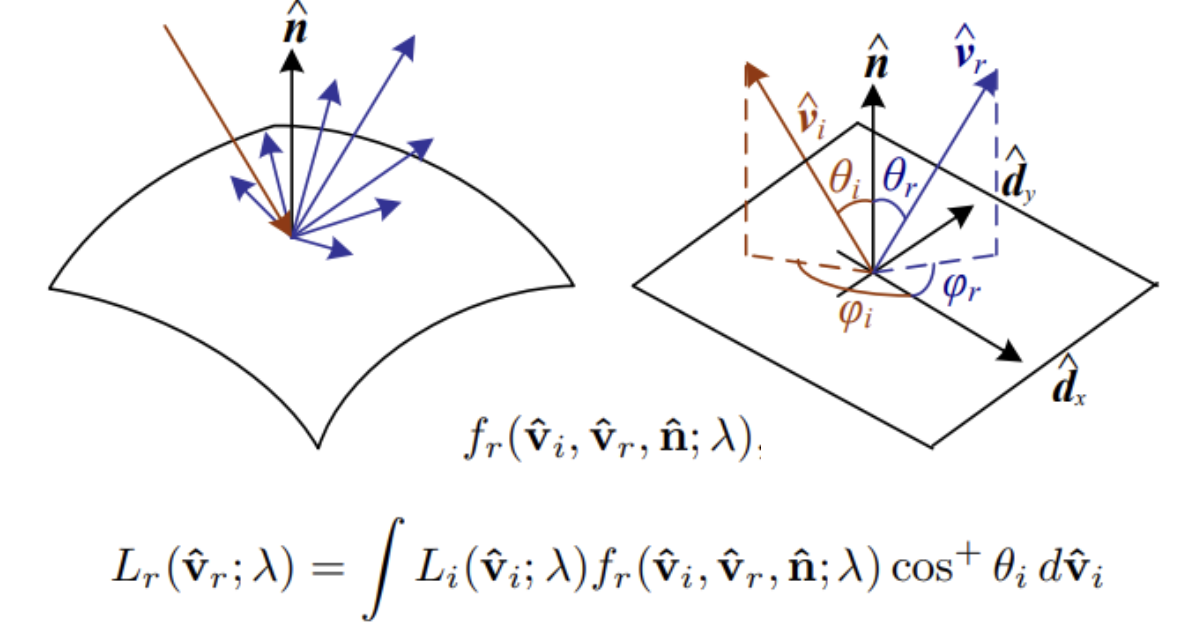
上式中 ${\hat{v}}_i$ 表示入射光线的方向，${\hat{v}}_r$ 表示反射光线的方向，$\hat{n}$ 表示表面法向量的方向，$\lambda$ 表示光线的波长，等式左端的结果 $L_r({\hat{v}}_r;\lambda )$ 表示以 ${\hat{v}}_r$ 方向射出的，波长为 $\lambda$ 的光线的强度