绪论

2025/9/16大约 4 分钟人工智能机器学习

机器学习导论

定义

以数据为经验的载体，利用经验数据不断提高性能的计算机系统/程序/方法

典型的机器学习过程

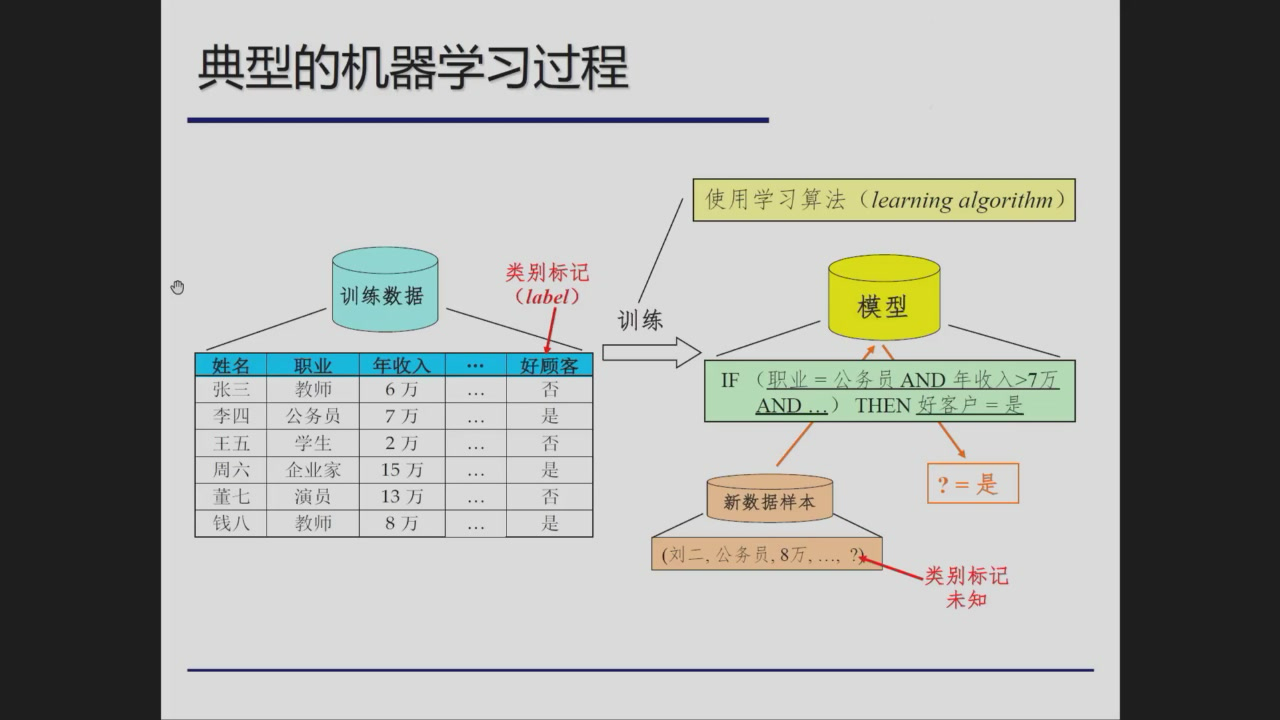
基本术语

学习过程

学习过程就是得到输入到输出的预测模型

数据

特征: 用来描述数据的可测量或可识别的属性或特性
特征
又称为属性、变量、输入
数据中的每一列(除了我们想要预测的目标列)通常就是一个属性
每一个特征代表了观察对象的一个特定方面的信息
特征值: 特征的离散取值或连续取值
样本维度(Dimensionality): 特征个数
特征张成的空间: 属性空间/特征空间/输入空间
标记张成的空间: 标记空间/输出空间
示例(Instance)/样本(Sample): 一个对象的输入，示例不含标记
样例(Example): 示例+标记
标记、样例
标记表示模型的输出，又称目标变量、响应变量
样例表示一个完整的数据单元，包含特征(输入)和标记(输出)
训练集 = 一组训练样例
测试集 = 一组测试样例

预测任务

根据标记的取值情况可以分为:
- 分类任务: 标记为离散值
  - 二分类: 例如 (好瓜，坏瓜) (正类，反类) (+1, -1)
  - 多分类: 例如 (冬瓜，南瓜，西瓜)
- 回归任务: 标记为连续值，例如瓜的成熟度
- 聚类任务: 标记为空值，对示例进行自动分组，例如本地瓜、外地瓜
根据标记的完整情况可以分为:
- (有)监督学习: 所有示例都有标记
  - 分类、回归
- 无监督学习: 所有示例都没有标记
  - 聚类
- 半监督学习: 少量示例有标记，大量示例没标记
- 噪声标记学习: 标记有，但不完全准确
- ...

目标

机器学习技术的根本目标是泛化能力

由于未来不可知，一般依靠历史数据来逼近模型的泛化能力

这一理论基于 I.D.D. 假设：历史和未来来自相同分布

I.D.D.

独立同分布(independent and identically distributed，I.D.D.):

指随机过程中，任何时刻的取值都为随机变量，如果这些随机变量服从同一分布，并且互相独立，那么这些随机变量是独立同分布。

概念学习

最理想的机器学习是学习到概念（人类可学习、可理解的）

现实中很困难，很多时候采用的是黑盒模型

假设空间

西瓜数据集

对于上述数据集，若学习的目标是“好瓜”，则可将假设空间表示为：

好瓜 \leftrightarrow (色泽 = ?) \land (根蒂 = ?) \land (敲声 = ?)

当“色泽”“根蒂”“敲声”分别有3、2、2种可能取值，则该假设空间的规模大小为 $4 \times 3 \times 3 + 1 = 37$

假设空间规模计算

在计算假设空间规模时，需要考虑与该特征无关的情况

因此上式中的4、3、3均由特征的可能取值数加1得到，最终的加1则来自于与所有特征都无关的情况

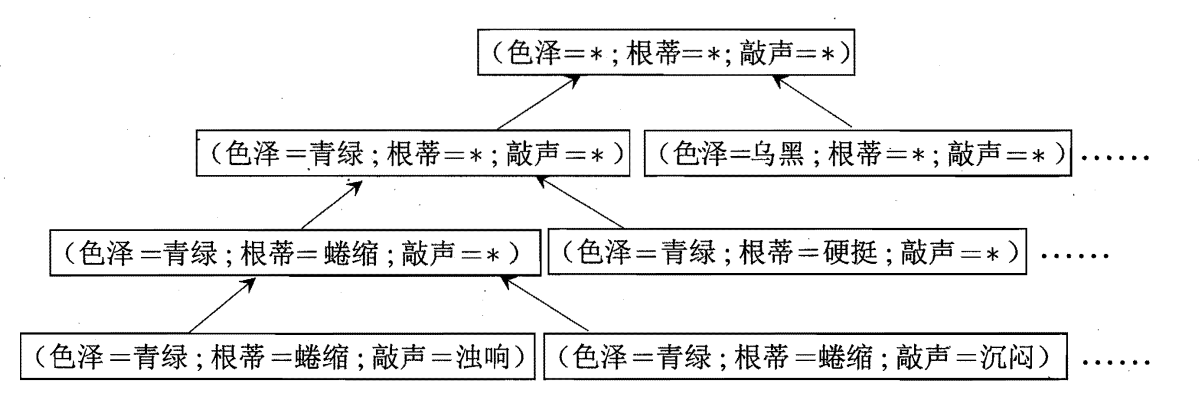
假设空间示意

版本空间

学习的过程是对假设空间中的错误假设进行删除，由于假设空间很大，训练集有限，因此可能存在多个假设与训练集一致，即版本空间（与训练集一致的假设集合）

版本空间示意

归纳偏好

机器学习算法在学习过程中对某种类型假设的偏好，任何一个有效的机器学习算法必有其归纳偏好

例如：算法可能喜欢"尽可能特殊"的模型，也可能喜欢"尽可能一般"的模型

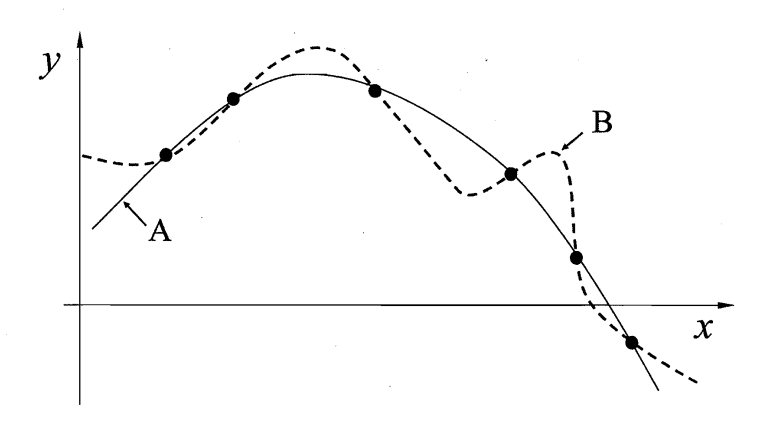
模型归纳偏好示意

NFL 定理

No Free Lunch (没有免费的午餐) 定理

一个算法 $L_{a}$ 如果在某些问题上比另一个算法 $L_{b}$ 好，必然存在另一些问题 $L_{b}$ 比 $L_{a}$ 好

在实际使用中，我们可能只注意问题的某些情况，因此，脱离具体问题，谈哪些算法更好毫无意义